学校の授業についていけない。コロナで学校を1週間休んだだけなのに、授業で何をやっているか全くわからない。
このような声を本当にたくさん聞きます。そんな方たちは必見!ここで苦手を克服できます!
今日の記事は中学2年生向けでこんな人におススメ!
・一次関数って何かわからない。
・1年生のときから数学・関数分野が苦手。
・定期テストで点数を取れないけど頑張って50点以上取りたい!
・まだ学校では授業をしていないけど、予習しておきたい。
私は中学生向けに数学の勉強法を載せています。解き方の解説、練習問題を含めすべての講義を15分程度で行えるようにしています。(※今回は少し長めになっています)
これを毎日やって定期テスト50点以上を目指しましょう!
もし、他の問題も練習してみたいなどリクエストがあればぜひコメントで教えてください!
私は10年間家庭教師として50名ほどの不登校の生徒・150名以上の中学生の勉強に携わり、指導を行ってきました。そんな私から、不登校の生徒様・勉強の苦手な生徒様に向け、勉強のノウハウをお伝えしていこうと思いますので、ぜひご覧ください!
そもそも関数とは?

カエデ先生、関数って何ですか?
関数とは2つの事がらのうち、1つがわかればもう1つも分かるよ。
というものです。関数は身近なところにもいっぱいあるのでいくつか例を出してみましょう。
料金が1人500円の動物園に友達と3人で行ったとしよう。
このとき3人でかかる料金は1,500円になります。
ここでいう2つの事がらとは、「人数」と「代金」になります。
ちなみに、人数・代金のようにそのときによって値が変わるもののことを「変数」というんです。
人数が変わったら、もちろん料金も変わりますよね?
その時に大事なのが、「1人500円」という情報がわかっていることです。
何人で行こうが、1人の値段が500円ということは変わりません。
このように、2つの事がらを決めるために、変わらない事がらを「定数」といいます。
こういった定数のことを「\(\displaystyle a\)」で表します。
定数があることによって、関数が成り立つのです。
今回の問題は、人数が決まったら代金が決まりました。
これを「代金は人数の関数である」といいます。
また、中学校では人数を\(\displaystyle x\)、代金を\(\displaystyle y\)として、
\(\displaystyle y\)は\(\displaystyle x\)の関数である
と表すのです。
結果を表すものを\(\displaystyle y\)、過程で使ったものを\(\displaystyle x\)とすることがほとんどなので覚えておきましょう。
※例外もあります。

じゃあ私が1時に寝て、そこから8時間寝る
っていうのも関数ってことねwwww

その通りです。それが一次関数ですね。
1時に寝て8時間寝たら起きるのは必ず9時になりますね。
これも関数といえるわけです。
1時に寝るというのが変わらない値(定数)
結果は起きる時刻(\(\displaystyle y\))
過程は寝ている時間(\(\displaystyle x\))は8時間となります。
一次関数って何?
中学生で習う関数には以下の4つがあります。
①比例(\(\displaystyle y=ax\))
②反比例(\(\displaystyle y=\frac{a}{x}\))
③一次関数(\(\displaystyle y=ax+b\))
④二次関数(関数\(\displaystyle y=ax²\))
④の二次関数(関数\(\displaystyle y=ax²\))については中学3年生で習うので、今回は省略させていただきます。
二次関数について学びたい方はコチラ!
①・②は中学1年生の内容なのでこちらも復習しつつ、一次関数について理解していきましょう!
① 比例(\(\displaystyle y=ax\))
比例とは(\(\displaystyle y\))が2倍・3倍になると(\(\displaystyle y\))も2倍・3倍になることです。
例としては最初の動物園のものや次のようなものがあります。

〔問題〕
時速8㎞で自転車をこいで\(\displaystyle x\)時間進むと\(\displaystyle y\)km先に到着した。
時速8㎞で1時間進むと進んだ道のりは8㎞。
時速8㎞で2時間進むと進んだ道のりは16㎞となります。
他にも、\(\displaystyle x\)と\(\displaystyle y\)の関係は次のように表すことができます。
| \(\displaystyle x\)(かかった時間) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ・・・ |
| \(\displaystyle y\)(進んだ距離) | 0 | 8 | 16 | 24 | 32 | 40 | 48 | ・・・ |
かかった時間(\(\displaystyle x\))が2倍になると進んだ道のり(\(\displaystyle y\))も2倍になっていますよね?
なので、\(\displaystyle y\)は\(\displaystyle x\)に比例するといえるのです。
ちなみに公式は\(\displaystyle y=ax\)です。
式で表すときは、定数の部分のみに数字をいれます。
問題を式で表すと \(\displaystyle y=8x\)とななるのです。
詳しくは下記の反比例の授業で説明しているので、
復習したい方はそちらから復習しておきましょう。
比例について詳しく学びたい方はコチラ!
② 反比例(\(\displaystyle y=\frac{a}{x}\))
反比例は\(\displaystyle x\)が2倍・3倍になると\(\displaystyle y\)は\(\displaystyle \frac{1}{2}\)倍,\(\displaystyle \frac{1}{3}\)倍になります。
ココでも例を挙げて説明しましょう。

〔例題〕
24Lの水が入る水槽に、1分間に\(\displaystyle x\)Lずつ水を入れていくと、\(\displaystyle y\)分で満水になった。
1分間に1Lずつ水を入れていくと、24分で満水になりますよね。
では1分間に3Lずつ水を入れていくとどうでしょう?
これがわかった人はもう大丈夫!
言い換えると、「24Lを3Lずつ分けると何分で満水になる?」ということですね。
そのため式は、24÷3=8 となります。
なので、1分間で3L ずつ水を入れていくと8分間で満水になります。
さあ、皆さんわかりましたか?
\(\displaystyle x\)(1分間に入れる水の量)が3倍になると、\(\displaystyle x\)(かかる時間)は\(\frac{1}{3}\)になっているので反比例の関係だといえるわけです。
ちなみに、\(\displaystyle x\)と\(\displaystyle y\)の関係は次のようになります。
| \(\displaystyle x\)(1分間に入れる水の量) | 1 | 2 | 3 | 4 | 6 | 8 | 12 |
| \(\displaystyle y\)(満水になるまでかかる時間) | 24 | 12 | 8 | 6 | 4 | 3 | 2 |
反比例の公式は\(\displaystyle y=\frac{a}{x}\)になります。
定数(変わらない数)は「24」なので、
この問題を式で表すと\(\displaystyle y=\frac{24}{x}\)ですね。
比例でもいいましたが、大事なことなのでもう一度言います。
式で数字を入れるのは定数(\(\displaystyle a\))の部分のみです。
もっと反比例について勉強したい人はコチラ!
③ 一次関数(\(\displaystyle y=ax+b\))

さあいよいよ本番の一次関数の内容です。
ココでの予習を少しだけ!
一次関数の公式は
\(\displaystyle y=ax+b\)
この\(\displaystyle a\)のことを「傾き」(※変化の割合ともいいます)
また\(\displaystyle b\)のことを「切片」といいます。
一次関数についても例を出して説明していきますね。

例で説明してもらったほうがイメージつくので助かります。
〈例題〉
200gのカバンの中に、100gの本を\(\displaystyle x\)冊いれるとカバンの重さは\(\displaystyle y\)gになる。
100gの本を1冊で100g、2冊で200gです。ここは理解できるでしょうか?
本の冊数が2倍になると、本の重さも2倍になります。
あれ?これって比例と一緒じゃないの?
と思った人もいるかもしれません。
実はまだ登場していないものがあるんです。
そう、カバンの重さです!
\(\displaystyle y\)は「カバンの重さ」なので、
本を1冊入れると、 本の1冊の重さ+カバンの重さ=300g
本を2冊入れると、 本の2冊の重さ+カバンの重さ=400g
本の冊数が2倍になっても、カバンの重さは2倍にはなっていませんよね?
表で整理して、特徴を考えてみましょう。
| \(\displaystyle x\)冊(本の冊数) | 0 | 1 | 2 | 3 | 4 | 5 | ・・・ |
| \(\displaystyle y\)g(カバンの重さ) | 200 | 300 | 400 | 500 | 600 | 700 | ・・・ |

なにか気づいたことはありますか?

100gずつ増えていることかなぁ。

さすが、まさにそこなんです。
Aさんが言っていた通り、
\(\displaystyle x\)の値が1増えると、\(\displaystyle y\)の値が100増えていますね。
このように、\(\displaystyle x\)の値が1増えるときに増える\(\displaystyle y\)の値を
傾き(\(\displaystyle a\))といいます。
グラフで表すとこのようになります。
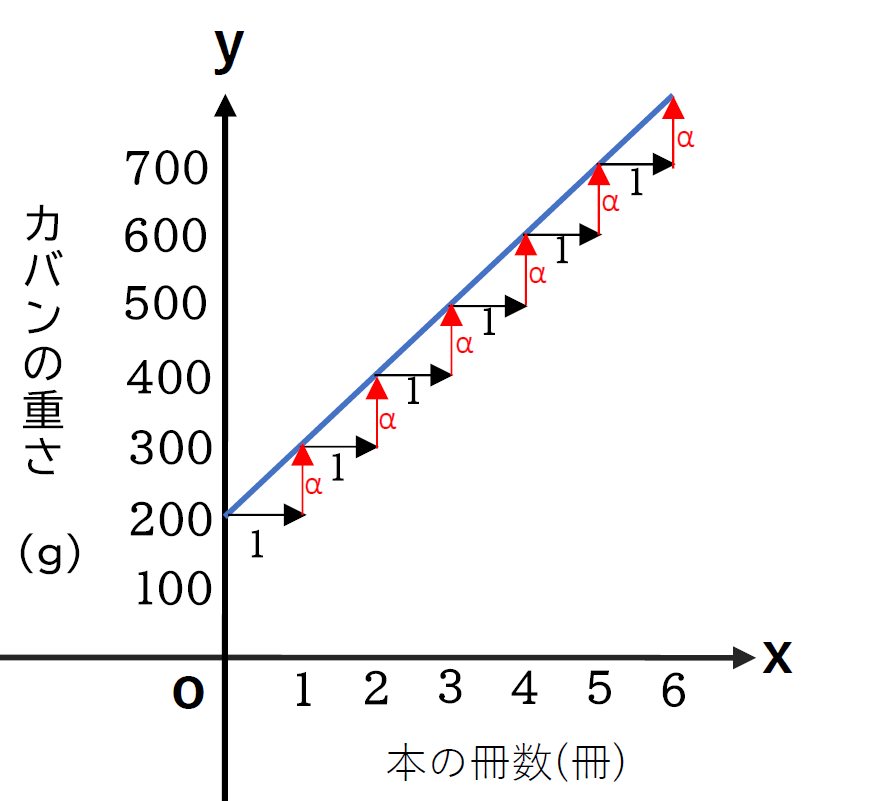
上のグラフのように一次関数のグラフは直線のグラフになります。
実は、もう一つ比例とは違うところがあります。
それは、グラフのスタート地点です。
\(\displaystyle x=0\)(\(\displaystyle y\)軸上)のとき\(\displaystyle y\)の値が「0」ではないのです。
この、\(\displaystyle x\)=0のときの\(\displaystyle y\)の値のことを切片(\(\displaystyle b\))といいます。
一次関数の公式は\(\displaystyle y=ax+b\)
\(\displaystyle a\)(傾き)と\(\displaystyle b\)(切片)は定数にあたるので、式で表すときは、
\(\displaystyle y=100x+200\)となるのです。
今回は2つありますが、式で表すとき数字を入れるのは定数\(\displaystyle a,b\)の部分のみですよ。
では最後にもう1つだけ。
比例は一次関数です。

え、、、、、?
誤解がないよう、こちらの表を見てください。
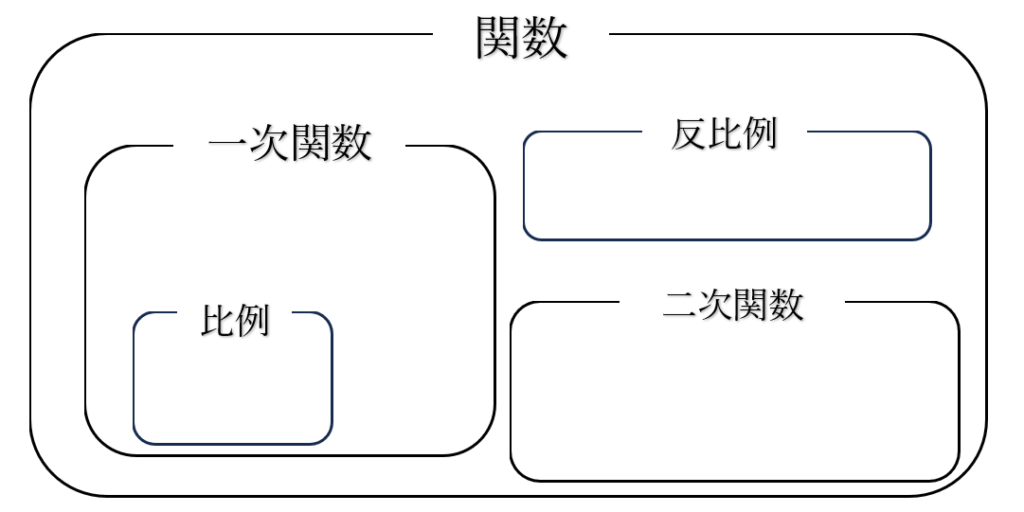
比例は一次関数の一部なのです。
比例の公式は \(\displaystyle y=ax\)
一次関数の公式は\(\displaystyle y=ax+b\)
2つの公式の違いは、「\(\displaystyle b\)」です。
比例は、一次関数\(\displaystyle y=ax+b\)の
\(\displaystyle b=0\)のパターンなのです。
比例とは、\(\displaystyle y=ax+0\)
先ほどの例題はこのようなものでした。
200gのカバンの中に、100gの本を\(\displaystyle x\)冊いれるとカバンの重さは\(\displaystyle y\)gになる。
この例題では、\(\displaystyle b=200g\)のカバンですが、
これが30gの袋だった場合はどうでしょう?
\(\displaystyle y=ax+30\)となりますよね。
では、本を自身の手で持つ場合はどうでしょう?
カバンなどはないので、プラスされる重さは0gなので、
\(\displaystyle y=100x+0\)となるわけです。
そのため、\(\displaystyle b=0\)のときの一次関数を「比例」というのです。
覚えておけるよう頑張りましょう!
さあ、わかった方は練習問題に挑戦してみましょう!
練習問題に挑戦(プリントPDF)
一次関数って何?練習問題.pdf
一次関数って何?解答.pdf
まとめ
今回の講義のまとめです。
〇比例の公式は\(\displaystyle y=ax\)
・\(\displaystyle x\)の値が2倍・3倍になると、\(\displaystyle y\)の値も2倍・3倍になります。
・また、一次関数\(\displaystyle y=ax+b\)の\(\displaystyle b\)が0のときも比例です。
・比例も一次関数の仲間だということを覚えておきましょうね。
〇反比例の公式は\(\displaystyle y=\frac{a}{x}\)です。
・\(\displaystyle x\)の値が2倍・3倍になると、\(\displaystyle y\)の値は\(\frac{1}{2}\)倍・\(\frac{1}{3}\)倍となります。
〇一次関数の公式は\(\displaystyle y=ax+b\)です。
・\(\displaystyle a\)=傾き(\(\displaystyle x\)が1増えたときの\(\displaystyle y\)が増える値のことをいいます。
・\(\displaystyle b\)=切片(\(\displaystyle y=0\)のときの\(\displaystyle x\)の値のことをいいます。\(\displaystyle b\)=スタート地点でしたね!
今回は覚えることが多かったですね。
次の講義から実戦で使っていきましょう!
次の講義はコチラ»»»



コメント