こんにちは。カエデです。
昨日、ニセコに行ってきました。
Pi-kan Rollpizzaさんでランチを
いただきましたが、

ここは絶品!
是非皆さんも
ニセコに行ったときは
寄ってみてください!
本日は文字式の重要語句に
ついて勉強していきます。
計算や文章問題などは
ありませんが、かなり
重要なものなので、
理解を深めていってほしいです!
この授業は4月から
中学2年生になった
こんな人向け。
・中1の文字と式も苦手だった。
・2年生では数学の評定を上げたい!
・クラス替えで友達作りに夢中で勉強ついていけない。。。
・数学苦手だけど得意になりたい!
・定期テストで50点以上を目指したい。
・学校に行ってないけど勉強はしたい。
1つでも当てはまった人は
最後まで見てください。
絶対に損はさせません!
カエデは、
北海道で家庭教師の会社で
10年ほど講師をしており、
勉強が苦手な生徒や不登校
になってしまった生徒を
中心に授業をしてきました。
そんな私が
少しでも勉強への苦手意識が
なくなるようにわかりやすく
1回10分ほどで勉強を教えて
いきますので、どうぞ見ていってください。
重要語句一覧
まずはそれぞれの言葉について簡単に説明していきます。
単項式・・・「+」や「-」で分けられず、かたまりが一つの式
多項式・・・「+」や「-」が間に含まれていくつかのかたまりに分けられている式
項 ・・・多項式の中にあるそれぞれのかたまり
定数項・・・文字が含まれていない項
次数 ・・・単項式にかけられている文字の個数
同類項・・・多項式の中の項で文字の種類が全く同じ項
これだけでは全く意味が
分からないですよねww
もっとわかりやすく説明していきます!
単項式と多項式とは
まずは、
多項式について説明していきます。
多項式とは
「+」や「-」が間に含まれて
いくつかのかたまりに分けられている式
ということでした。
例えばこんな式
\(\displaystyle 3x+2y-5\) \(\displaystyle -4x²+9x\)
まず、「+」や「-」が間に含まれるとは
このようなことです。

文字や数字の間が、
「+」や「-」で
わかれていますよね。
次に、
いくつかのかたまりで分けられているとは
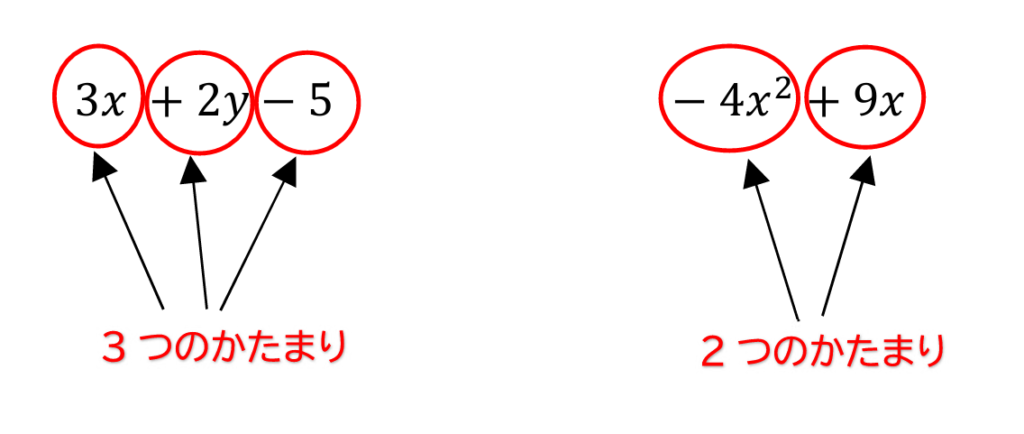
「+」「-」をいれて分けると
このようにできます。
では、単項式は?
単項式とは、
「+」や「-」で分けられず、
かたまりが一つの式でした。
多項式の説明を聞いて
わかった人もいるかも
しれませんが、
こんな式です。
①\(\displaystyle 3x\) ②\(\displaystyle -4x²\)
このように、
かたまりが一つだけの式のことです。
単項式は「項」が単体で存在する式。
多項式は「項」が多数存在する式。
ともいうことができますね!
では、
「項」とは?
項と定数項とは
項とは
項とは、
ズバリ「かたまり」のことです。
先ほどまで乱用していた「かたまり」ですね。
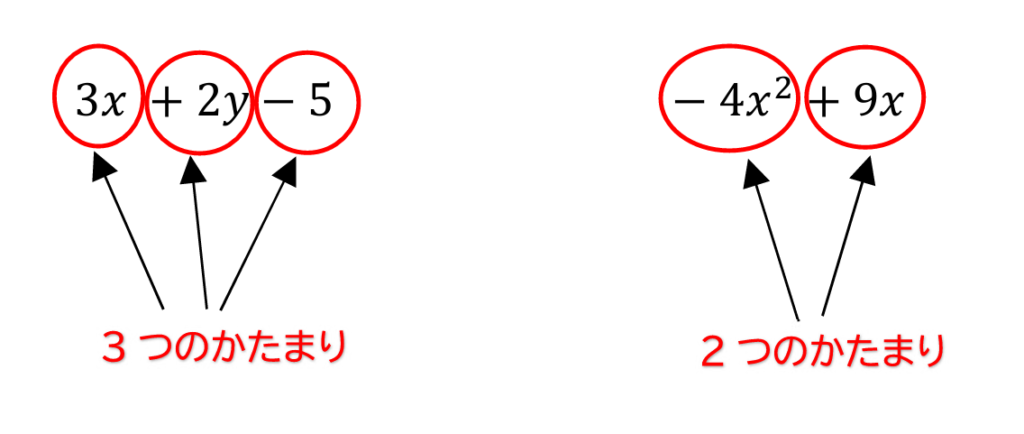
この「かたまり」が「項」なのです。
なので、先ほどの
\(\displaystyle 3x+2y-5\)の項を答えてください。
という問題があれば
\(\displaystyle 3x\)と\(\displaystyle 2y\)と\(\displaystyle -5\)
と答えれば正解です!
※それぞれの項を答えるとき、「+」は省きます。
\(\displaystyle -4x²+9x\)の項を答えてください。
この問題ももう簡単ですね!
答えは \(\displaystyle -4x²\)と\(\displaystyle 9x\)
ですね。
定数項とは
定数項とは、
文字が含まれていない項のことです。
先ほどの\(\displaystyle 3x+2y-5\)
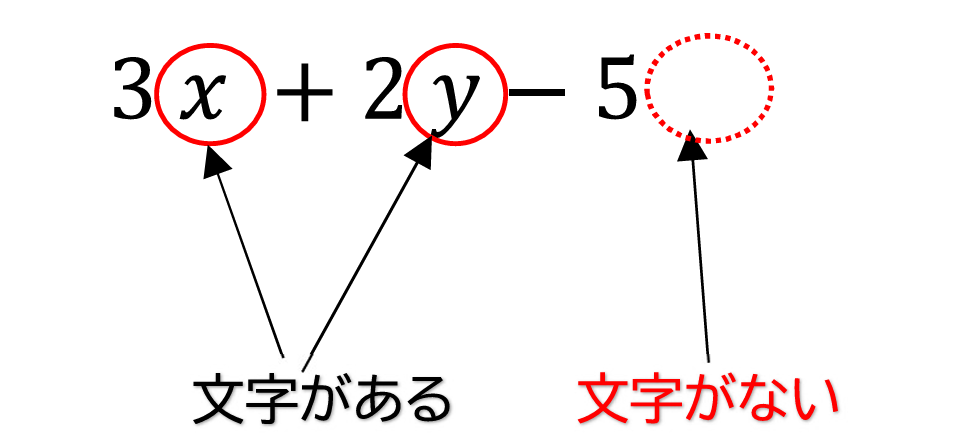
\(\displaystyle -5\)は
文字がない項ですね。
なので、定数項は \(\displaystyle -5\)
となります。
文字がない項を見つければ
良いのでここはそんなに
難しくないですね。
次数とは
次数とは、
単項式にかけられている
文字の個数でしたね!
例えば、この単項式の次数は?
\(\displaystyle 5xy²\)
これをかけ算の式に直すと、
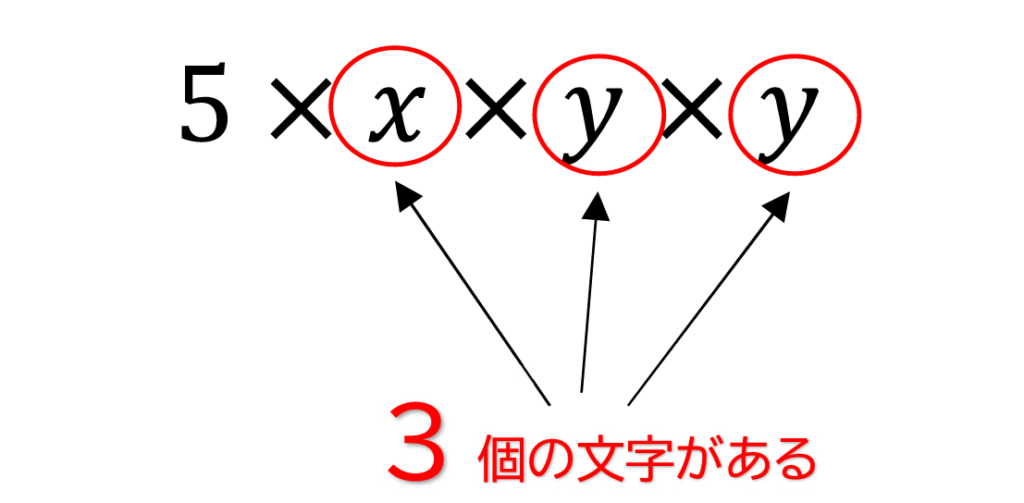
こうなります!
かけられている文字は3個
なので\(\displaystyle 5xy²\)の次数は
3 となります。
また、次数が3の式を
3次式といいます。
次数が1の式・・・1次式
次数が2の式・・・2次式
次数が4の式・・・4次式
というように次数によって
式の名前が変わるので
必ず覚えておきましょう!
\(\displaystyle 5xy²\)の次数は?
という問題なら→3
\(\displaystyle 5xy²\)は何次式?
という問題なら→3次式
と答えなければならないので
問題を読んでくださいね!!
その多項式は何次式?
では、多項式ならどうでしょう?
多項式では、それぞれの
項の中でもっとも次数が
大きいものをつかいます。
例えば、
\(\displaystyle -6x³+2x-9\)は何次式ですか?
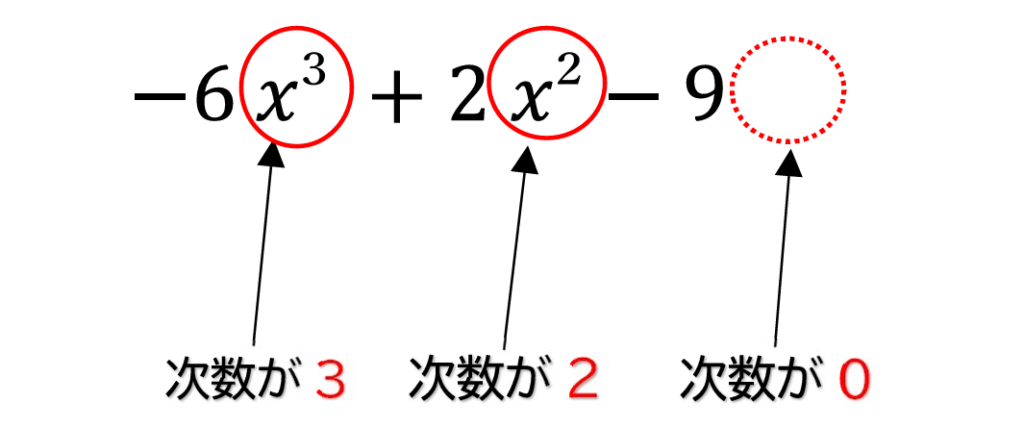
これ、5次式じゃないんです!
多項式は次数がもっとも大きい
項のものを使います。
\(\displaystyle -6x³\)の次数が
最も大きいので、
\(\displaystyle -6x³+2x-9\)
は3次式となります。
同類項とは
同類項とは、
多項式の中の項で
文字の種類が全く
同じ項のことです。
専門用語が増えて
きていますが、
ついてこれてますか?
わからなくなったら
もう一度上に戻って
確認してみてください。
では、同類項ついて
解説していきます!
例題:\(\displaystyle -6a+2b-a+5b\)の同類項を答えてください。
各項についている
文字の種類が同じ
ものを探していきます。
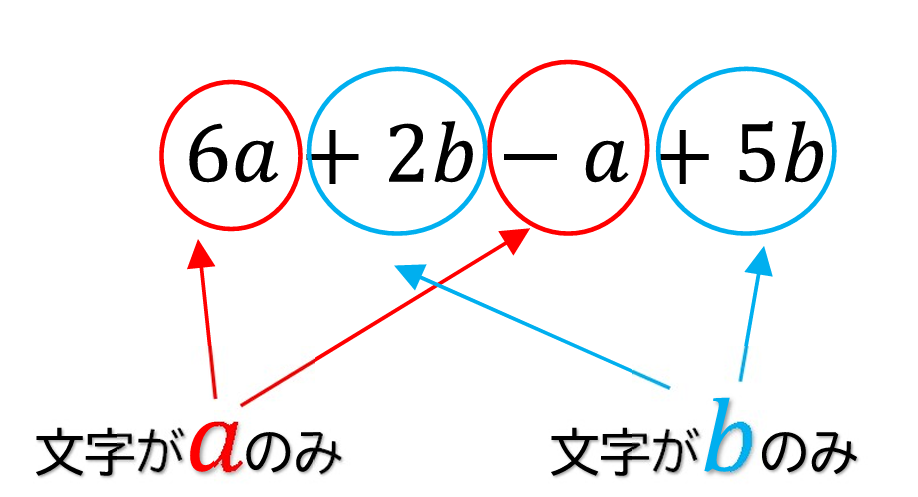
もうわかりましたね?
同類項は
\(\displaystyle -6a\)と\(\displaystyle -a\)
\(\displaystyle 2b\)と\(\displaystyle 5b\)
ということになります。
た だ し !
\(\displaystyle -6a²+2b-a+5b\)
こんな式の場合は
\(\displaystyle -6a²\)
についている文字は→\(\displaystyle a×a\)
\(\displaystyle -a\)
についている文字は→\(a\)のみ
よって、
\(\displaystyle -6a²\)と\(\displaystyle -a\)
は同類項とは言えません!
文字の種類が
全く同じでないと
いけないのです。
まとめ
では本日のまとめです。
最初と同じものを載せますが、
いまなら15分前よりも確実に
理解が深まっているはずです!
単項式・・・「+」や「-」で分けられず、かたまりが一つの式
例:\(\displaystyle -6a\) \(\displaystyle 3xy²\)
多項式・・・「+」や「-」が間に含まれていくつかのかたまりに分けられている式
例:\(\displaystyle 3x+4y\) \(\displaystyle -a²+3a-5\)
項 ・・・多項式の中にあるそれぞれのかたまり
定数項・・・文字が含まれていない項
次数 ・・・単項式にかけられている文字の個数
同類項・・・多項式の中の項で文字の種類が全く同じ項
理解できなかった人は
もう1回見てみましょう。
反復はとても大切です!!



コメント