こんにちは。カエデです。
本日の授業は中2数学、
多項式の加法と減法についてです。
このページはこんな人向け!
・GWで計算問題をできるようにしたい!
・定期テストで平均点を取りたい!
・計算問題が苦手、、、
・不登校だけ勉強したい!
・中1の復習もしたい!
1つでも当てはまった方は
最後まで見ていってください。
15分後にはできることが
必ず増えています!
同類項とは
今回は、同類項について詳しく勉強します。
重要語句の復習
前回の復習をしていきましょう。
項 ・・・文字や数がかけられている1つのかたまり
単項式・・・項が1つだけの式
多項式・・・項が2つ以上の式
次数 ・・・項にかけられている文字の数
同類項・・・かけられている文字の種類が全く同じ項
同類項について詳しく知ろう
今回は、同類項について
詳しく見ていきます。
重要語句にあった同類項の
文字の種類が全く同じとは
・文字の種類が同じ
・次数が同じ
この2つが必要です。
3つの例で説明していきます。
例題:同類項を答えましょう。
①\(\displaystyle 3x+5y-9x\)
②\(\displaystyle x²+2y²+7x-y²\)
③\(\displaystyle 3ab²-a²b\)
①\(\displaystyle 3x+5y-9x\)
では同類項は\(\displaystyle 3x\)と\(\displaystyle -9x\)
②\(\displaystyle x²+2y²+7x-y²\)
では同類項は\(\displaystyle 2y²\)と\(\displaystyle -y²\)です。
と\(\displaystyle 7x\)は?
\(\displaystyle x²\)の次数は2
\(\displaystyle 7x\)の次数は1
と次数が違うので、
同類項ではありません。
同じく、
③\(\displaystyle 3ab²-a²b\)
\(\displaystyle 3ab²\)=\(\displaystyle 3×a×b×b\)
\(\displaystyle -a²b\)=\(\displaystyle -a×a×b\)
とかけられている文字の種類が違うので
この多項式には同類項はありません。
では、この同類項って
そんなに重要なのか?
とても重要です。
なぜなら同類項は
まとめることができるのです!
同類項をまとめる
同類項をまとめるとは
どういうことなのか?
同類項どうしは、たすことができる
ということです。
\(\displaystyle 3x+5x=8x\)
これは、中1でも勉強したので
覚えている人も多いのでは?
忘れてしまった人はコチラを
確認してみましょう。
文字式の計算①
同類項をまとめるときのポイントはこの4つです。
〇 同符号の項→たす 異符号の項→ひく
〇 答えの符号→絶対値の大きい数の符号
〇 最初の項に「+」は書かない
〇 係数が「1」の場合は1と書かない
例題:同類項をまとめましょう。
① \(\displaystyle -3xy+4xy\)
② \(\displaystyle 7x²+3x-2x²\)
③\(\displaystyle 4x-1+2x+6\)
① \(\displaystyle -3xy+4xy\)
\(\displaystyle -3xy\)と\(\displaystyle 4xy\)は同類項なので
まとめることができます。
\(\displaystyle -3xy\)と\(\displaystyle +4xy\)は
・異符号なので「4(大きい数)-3(小さい数)」
=1 (1は書かない)
・\(\displaystyle +4xy\)のほうが大きいので
符号は「+」(最初の+は書かない)
\(\displaystyle -3xy+4xy\)
\(\displaystyle =xy\)
となります。
② \(\displaystyle 7x²+3x-2x²\)
同類項は \(\displaystyle 7x²\)と \(\displaystyle -2x²\)
※\(\displaystyle 3x\)は次数が違うので同類項ではないので、
計算せずにそのまま書く。
\(\displaystyle 7x²\)と\(\displaystyle -2x²\)は
・異符号なので「\(\displaystyle 7\)(大きい数)-\(\displaystyle 2\)(小さい数)」
=\(\displaystyle 5\)
\(\displaystyle 7x²\)のほうが大きいので
・符号は「+」(最初の+は書かない)
\(\displaystyle 7x²+3x-2x²\)
\(\displaystyle =5x²+3x\)
③\(\displaystyle 4x-1-2x+6\)
同類項は\(\displaystyle 4x\)と\(\displaystyle 2x\)
\(\displaystyle -1\)と\(\displaystyle 6\)
※定数項は次数が\(\displaystyle 0\)の同類項です
\(\displaystyle 4x\)と\(\displaystyle 2x\)は
・同符号なので「\(\displaystyle 4+2\)」
=\(\displaystyle 6\)
・\(\displaystyle 4x\)のほうが数が大きいので
・答えの符号は「+」(最初の+は書かない)
\(\displaystyle -1\)と\(\displaystyle 6\)は
・異符号なので「\(\displaystyle 6\)(大きい数)-\(\displaystyle 1\)(小さい数)」
=\(\displaystyle 1\)
・\(\displaystyle +6\)のほうが数が大きいので
・答えの符号は「+」
2つをまとめると
\(\displaystyle 4x-1-2x+6\)
\(\displaystyle =6x+5\)
となります。
このように、
同類項をまとめるとは
同じ種類の項をみつけて
足したり引いたりすることです。
ポイントもしっかり
押さえておきましょう!
〇 同符号の項→たす 異符号の項→ひく
〇 答えの符号→絶対値の大きい数の符号
〇 最初の項に「+」は書かない
〇 係数が「1」の場合は1と書かない
中1とのちがい
中1と何がかわったの?
そんな風に思うかもしれません。
かわったのはただ1つです。
1つの式に文字の種類が増えたこと。
これだけなんです。
中1の計算問題は
\(\displaystyle (3x+2)-3(2xー1)\)
中2の計算問題は
\(\displaystyle (3x+2y)-3(2x-y)\)
という感じに
中1は文字の種類が1種類
中2は文字の種類が2種類以上
にかわるだけなので
根本的な計算方法は何もかわりません!
多項式の計算
多項式の加法の流れ
多項式の加法とは
こんな式です。
例題:次の計算をしてください。
\(\displaystyle (3x+2y)+(x-7y)\)

さっきの同類項をまとめる問題と
何がちがうの?

( )がついている以外は
何も変わらないんですよ!
多項式の加法は
この順序で解きます。
①( )を外す
②同類項をまとめる
( )を外す方法について
詳しく見ていきます。
今回説明する( )を外す方法は、
大きく分けて4通りです。
〇 ( )の前に何もないパターン
〇 ( )の前に「+」があるパターン
〇 ( )の前に「-」があるパターン
〇 ( )の前に「数字」と「+」か「-」があるパターン
( )の前に何もない ( )の前に「+」がある
( )の前に何もないパターンと
( )の前に「+」があるパターンです。
\(\displaystyle (4x-3)+(2x+1)\)
のような式ですね。
これは結論
( )の前に何もないものは
そのまま外します。
\(\displaystyle (4x-3)\)
=\(\displaystyle 4x-3\)
となるのです。
( )の前に「+」があるものは
「+」を無視してそのまま外します。
※( )の中の最初の項が「+」の場合、
「+」をつけて( )を外す。
\(\displaystyle +(2x+1)\)
=\(\displaystyle +2x+1\)
これを一つにすると
\(\displaystyle (4x-3)+(2x+1)\)
( )を外す
=\(\displaystyle 4x-3+2x+1\)
同類項をまとめる
=\(\displaystyle 6x-2\)
このようになります。
( )の前に「-」がある ( )の前に「数字」がある
( )の前に数字があろうと
「-」があろうとやることは
先ほどと同じです。
①( )を外す
②同類項をまとめる
( )を外す方法が
違うので、復習していきましょう。
例題:次の式を計算しましょう。
\(\displaystyle -(x-y)\)+2\(\displaystyle (2x+3y)\)
\(\displaystyle -(x-y)\)は
( )の前に「-」があります。
その場合は、
( )の中の項の
符号をチェンジします。
まずは
\(\displaystyle -(x-y)\)
\(\displaystyle x\)の符号は
見えていませんが、
「+」なので、「-」にチェンジ
\(\displaystyle -x\)
\(\displaystyle -y\)の符号は
「-」なので「+」にチェンジ
\(\displaystyle +y\)
\(\displaystyle -(x-y)\)
=\(\displaystyle -x+y\)
次に
+2\(\displaystyle (2x+3y)\)
( )の前に数字があります。
その場合は
分配法則で( )の中の項
それぞれにその数を掛けます。
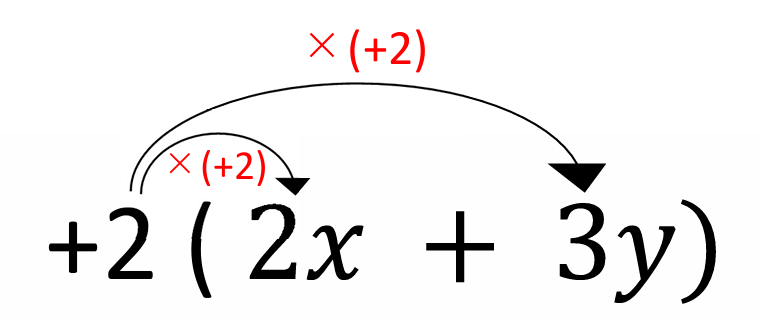
このようにそれぞれの項に
×(+2)をしていきます。
掛けるときは文字はそのままで
数字と符号のみ計算をしていきます。
\(\displaystyle +2×2x\)
=\(\displaystyle 4x\)
\(\displaystyle +2×3y\)
=\(\displaystyle +6y\)
\(\displaystyle +2(2x+3y)\)
=\(\displaystyle 4x+6y\)
この2つをまとめると
\(\displaystyle -(x-y)\)\(\displaystyle +2(2x+3y)\)
=\(\displaystyle -x+y+4x+6y\)
では次に同類項を
まとめていきます。
\(\displaystyle -x+y+4x+6y\)
の同類項は
\(\displaystyle -x\)と\(\displaystyle 4x\)
\(\displaystyle y\)と\(\displaystyle 6y\)
これを一連の流れであらわすと
\(\displaystyle -(x-y)\)\(\displaystyle +2(2x+3y)\)
( )を外す
\(\displaystyle -x+y+4x+6y\)
同類項をまとめる
=\(\displaystyle 3x+7y\)
こんな感じで、
①( )を外す
②同類項をまとめる
この流れはとても大事!!
本日のまとめ
本日のまとめです。
同類項とは、
文字の種類と次数が全く同じ項
同類項をまとめる
同類項はまとめることができる!
計算のポイントはこの4つ。
〇 同符号の項→たす 異符号の項→ひく
〇 答えの符号→絶対値の大きい数の符号
〇 最初の項に「+」は書かない
〇 係数が「1」の場合は1と書かない
( )の外し方
( )の外し方も4パターン
必ず覚える!!
〇 ( )の前に何もないパターン
→そのまま外す。
〇 ( )の前に「+」があるパターン
→そのまま外す。必要なら「+」も書く
〇 ( )の前に「-」があるパターン
→( )の中の項の符号をチェンジ!
〇 ( )の前に「数字」と「+」か「-」があるパターン
→分配法則
( )の中の数字をそれぞれの項に掛ける
かなりボリュームがあったけど
理解できたら次に進みましょう!!



コメント