こんにちは。カエデです。
本日の授業は多項式の
2種類の難しい問題に
チャレンジしてしょう!
今回は
分配法則を使った計算
これを本日で
マスターしてもらいます!
本日の内容はこんな人向け!
・小学生の時から聞いてるけど、よくわかんないんだよなあ。
・定期テストで70点以上取りたい!
・わかっているつもりだけどなぜか自分でやるとできない。
・不登校だけど学校に行ったときにできる奴と思われたい!
1つでも当てはまる方は
最後まで見てくださいね!
カエデは家庭教師として10年間
不登校の中学生や勉強が苦手な
中学生に少しでも勉強ができる
ようにと教えてきました。
この内容をあなたの参考書として
1つ勉強の苦手をなくしましょう!
前回の復習
前回の復習として( )の外し方を
思い出してください。超大事です!
〇 ( )の前に何もないパターン
→そのまま外す。
〇 ( )の前に「+」があるパターン
→そのまま外す。必要なら「+」も書く
〇 ( )の前に「-」があるパターン
→( )の中の項の符号をチェンジ!
〇 ( )の前に「数字」と「+」か「-」があるパターン
→分配法則
( )の中の数字をそれぞれの項に掛ける
分配法則の練習
まずは分配法則について
おさらいしていきます。
分配法則とは
\(\displaystyle 2(2x+3y)\)
のように
( )の前に数字があるとき
その数字を( )の中の全ての
項にかけてあげることです。
\(\displaystyle 2\)と( )の間に
「×」があり、それぞれにかけることで
( )を外すイメージでOKですよ。
この場合は( )の前に
「2」があるので、
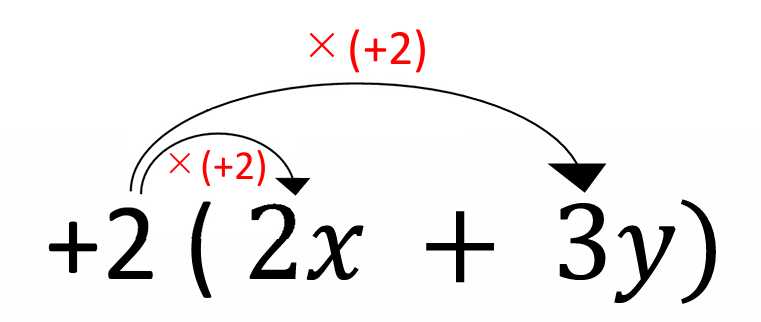
\(\displaystyle +2×2x\)
\(\displaystyle +2×3y\)
とそれぞれ計算していくのです。
\(\displaystyle 2(2x+3y)\)
=\(\displaystyle +2×2x+2×(+3y)\)
=\(\displaystyle 4x+6y\)
となります。
分配法則で計算できる理由
なぜそれが成り立つか?
数字を使って確かめてみましょう!
\(\displaystyle 2(2+3)\)
分配法則を使うと
=\(\displaystyle 2×2+2×3\)
かけ算から計算
=\(\displaystyle 4+6\)
=10
では次に( )の中から
計算してきましょう。
\(\displaystyle 2(2+3)\)
( )の中を計算
=\(\displaystyle 2×5\)
=10
このように答えは同じになるんですね。
( )から計算したほうが
早いし楽じゃん!
と思うかもしれませんが、
文字式ではそうはいかないのです。
\(\displaystyle 2(2x+3y)\)
この式では、
\(\displaystyle (2x+3y)\)
は同類項が違うので
計算できません。
そのため、多項式の計算は
分配法則を用いて行います。
わり算の分配法則
わり算の分配法則についても
勉強していきましょう。
※分配法則ができない場合もあるので
より詳しく学びたい方はコチラ!
ここで学習する方法について
先ほどのかけ算の分配法則と
それほど変わりません。
2つの例題を使って確認していきます。
例題:次の計算をしましょう。
① \(\displaystyle (-12x+9y)÷3\)
②\(\displaystyle (-21x+10y)÷(-3)\)
①\(\displaystyle (-12x+9y)÷3\)
これを分配法則で
計算するとこんな感じ。
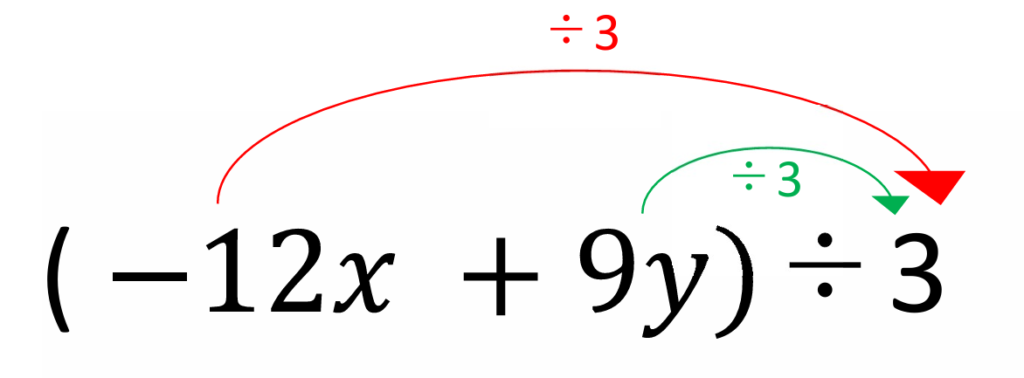
わり算の分配法則は
わる数が左側にくるので
その数で割ってあげます。
\(\displaystyle (-12x+9y)÷3\)
分配法則を使うと
=\(\displaystyle -12x÷3+9y÷3\)
=\(\displaystyle -4x+3y\)
②\(\displaystyle (-21x+10y)÷(-3)\)
そんなに変わらないように見えますが
この問題は少しクセがありますよ。
まず、①と同じように
分配法則をしていくのですが、
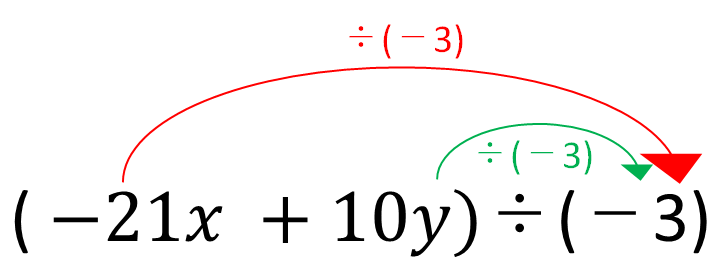
これを行うときに、
\(\displaystyle (-21x+10y)÷(-3)\)
=\(\displaystyle -21x÷(-3)+10y÷(-3)\)
ここで、
あれ?
\(\displaystyle 10y÷(-3)\)
って計算できなくね?
と思った方もいるかもしれません。
そう、ここがポイントです。
この場合は、わり算を
かけ算になおしてあげましょう!
※\(\displaystyle 0.33333y\)などとしないでくださいね。
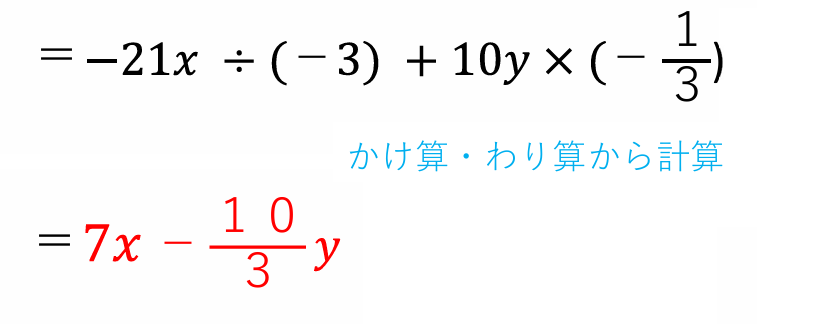
先にわり算になおしてから
でもOKですよ!
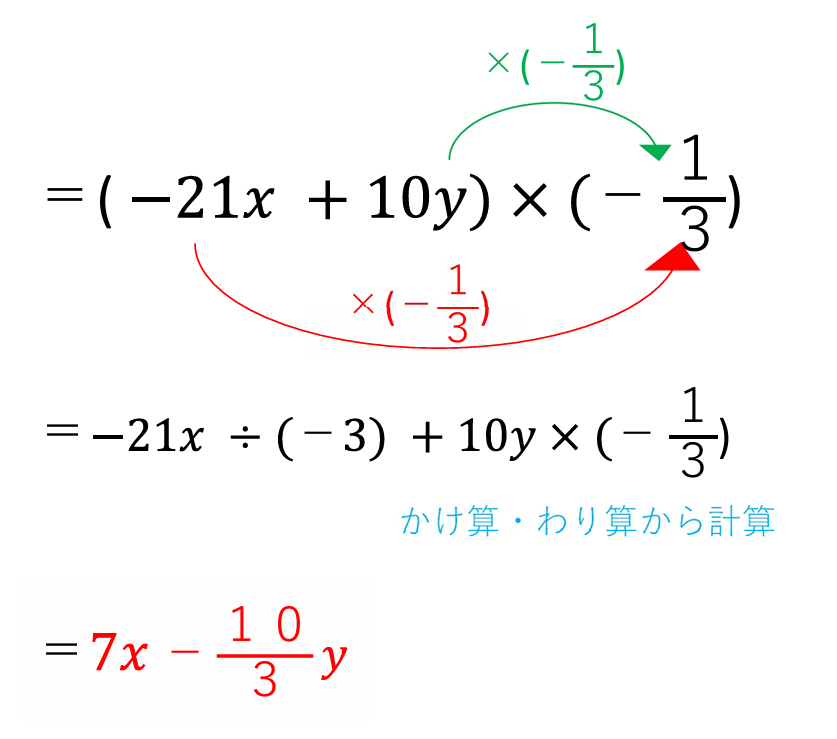
こんな感じで
わり算の分配法則を計算する場合、
かけ算になおすことで確実に解く
ことができるので覚えておきましょう。
練習問題
練習問題を行い、確実に
自力でできるように
勉強していきましょう。
分配法則の計算 問題
分配法則の計算 解答
本日のまとめ
分配法則について理解できたでしょうか?
分配法則とは
( )とセットになっている数で
かけたり割ったりすること。
そのとき、( )の中の
それぞれの項で計算する。
このことを理解できれば
計算問題でできることが
確実に増えていきます!



コメント