こんにちは。カエデです。
本日は正の数と負の数の
乗法についてお話をします。
乗法ってなに?
って不安に思ったひとも
安心してくださいね!
乗法っていうのは、
すばりかけ算のことです。
小学校2年生から習っている
かけ算に少しルールが加わるので
ここで確実に覚えておきましょう!
本日のお話はこんな人向け!
・かけ算のルールを早めに知っておきたい!
・符号の計算にとまどっている、、、
・最初の定期テストで50点以上取りたい!
・覚えてると思うけど説明することはできない。
1つでも当てはまった方は
最後まで見てください。
できない・不安な気持ちが
1つなくなりますよ!
1. 正負の数の乗法のルール
正負の数の乗法を行うには、
それぞれ計算のルールがあります。
これらは今後数学を学ぶ上で基礎となる
とても基本的かつ重要なルールですので、
ここでしっかりと身につけておきましょう。
2.1. 同符号の乗法
同符号の数をかけ算する場合、
結果は常に正の数になります。
(+)×(+)=(+)になるのは
なんとなくわかると思います。
1つ目の(+)は正の向きに
2つ目の(+)は進むことを表しているのです。
では、(-)×(-)=(+)に
なるのはなぜでしょう?
反対の反対は元に戻るからです。
今回の2つの符号は、
1つ目の(-)は負の向きに
2つ目の(-)は戻ることを表します。
よりわかるよう例題で
説明していきます。
例題:次の計算をして下さい。
① (+2)×(+3) ② (-2)×(-3)
①1つ目は(+)なので正の向きに。
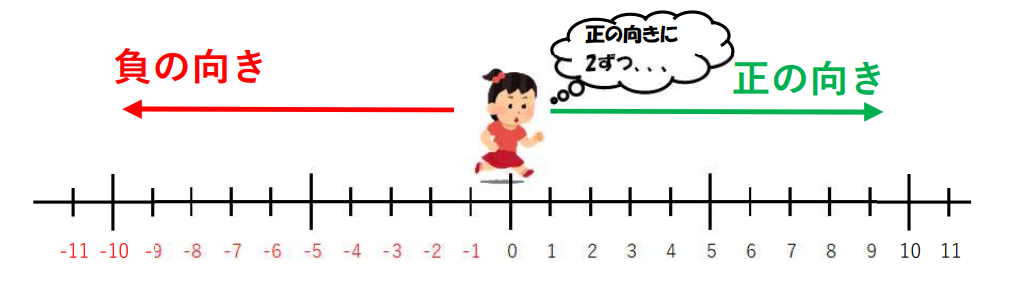
2つ目も(+)なのでその向きに進む。

「正(+)の向きに2ずつ」「3回進む(+)」
2つのことから
(+)×(+)=(+)
となることがわかりましたね。
よって、(+2)×(+3)=+6
では、②ではどうでしょうか?
1つ目は(-)なので負の向きに。
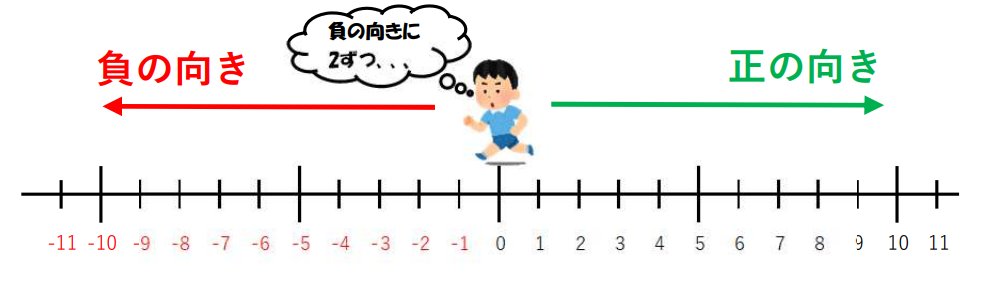
2つ目も(-)なのでその向きに戻る。
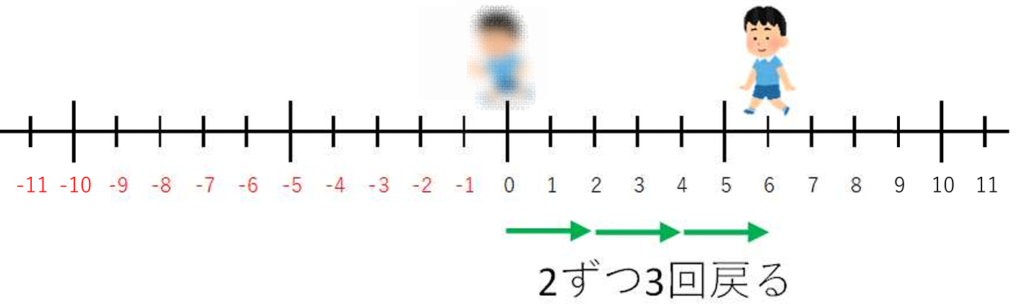
反対の反対で元に戻りましたね!
このことから、
(-)×(-)=(+)
であることも分かりました。
よって②の答えは
(-2)×(-3)=+6
同符号のかけ算は正の数になる!
理解できましたね!
異符号の乗法
異符号の乗法は
結果が必ず負の数になります。
もう一度復習しておきましょう。
1つ目の符号は向き
(+)なら正の向き
(-)なら負の向き
2つ目の符号は
(+)なら進む
(-)なら戻る
これをもとに考えていきますよ!
例題:次の計算をして下さい。
① (+2)×(-3) ② (-2)×(+3)
① 1つ目の符号は(+)なので正の向きに
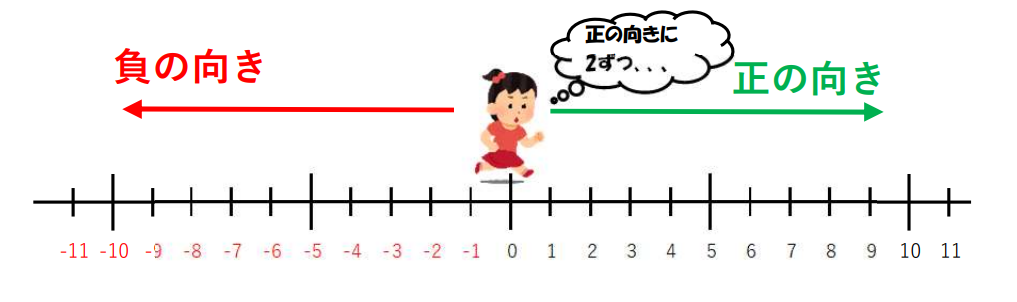
2つ目の符号は(-)なので戻る
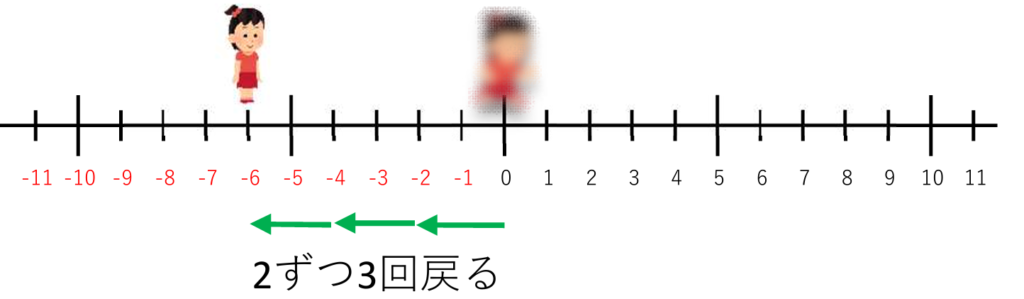
(+)×(-)=(-)でしたね!
このことから、
(+2)×(-3)=-6
②も同じように、
1つ目の符号は(-)なので、負の向きに
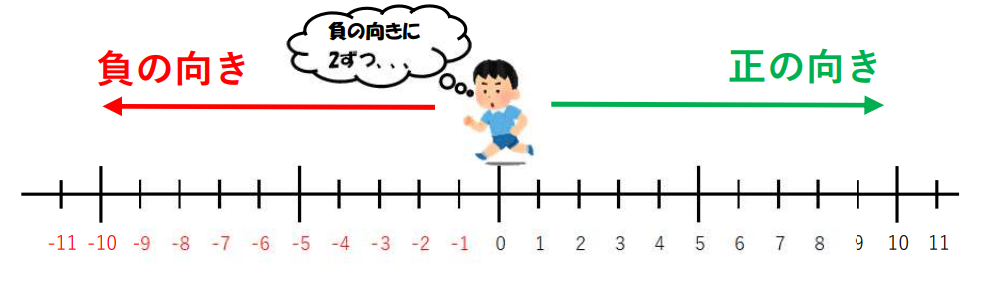
2つ目の符号は(+)なので、進む
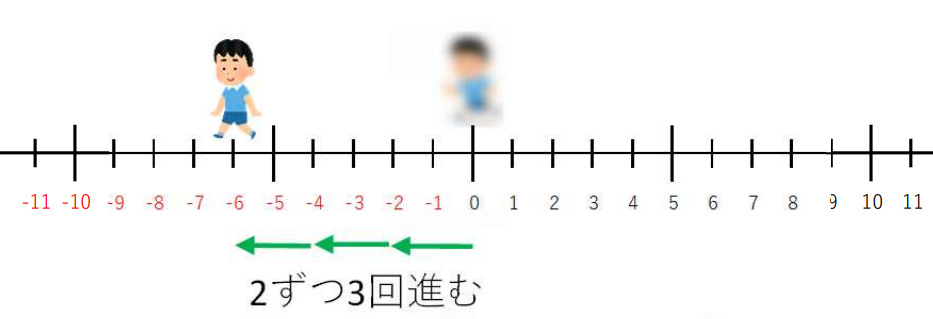
したがって、
(-)×(+)=(-)になります。
答えは(-2)×(+3)=-6
これで符号の計算はバッチリ!
(-)が3つ以上の乗法
まずはおさらい。符号の計算は
(+)×(+)=(+)
(-)×(-)=(+)
(+)×(-)=(-)
(-)×(+)=(-)
同符号のかけ算の積は正の数(+)
異符号のかけ算の積は負の数(-)
この2つはもう覚えましたか?
では、
(-)×(-)×(-)=??
この式だと、どうなるでしょう?
(-)×(-)×(-)
= (+) × (-)
=(-)
そう、(-)が3回ある場合、
答えはマイナス(-)になります。
じゃあこの問題なら?
(-)×(-)×(+)×(-)×(-)
= (+) × (+)×(-) ×(-)
= (+) × (-) ×(-)
= (-) × (-)
=(+)
(-)が4つかけられていたら
答えはプラス(+)になりましたね。
でも面倒くさくないですか?笑
実はこれ、簡単な方法があるんです!
(-)が偶数個・・・答えは正の数(+)
(-)が奇数個・・・答えは負の数(-)
これだけなんです。
さっきの面倒くさかった問題も
(-)×(-)×(+)×(-)×(-) …(-)が4つ(偶数)
=(+)
めちゃくちゃ簡単じゃないですか?
これ、完璧にしましょう。
本日のまとめ
乗法のルールは理解できましたか?
数字の計算は小学生の
時と変わらないので、
符号の計算のやり方を
再度確認しましょう!
(+)×(+)=(+)
(-)×(-)=(+)
(+)×(-)=(-)
(-)×(+)=(-)
(+)×(+)や(-)×(-)などの
同符号の計算は答えが必ず
正の数(プラス)になります!
(+)×(-)や(-)×(+)などの
異符号の計算は答えが必ず
負の数(マイナス)になる!
さらに、3つ以上の計算のときは
マイナスの数を確認するんですね!
マイナスの数が奇数個→答えはマイナス
マイナスの数が偶数個→答えはプラス
これさえ覚えておけば
正の数と負の数の乗法はカンペキ!!



コメント