こんにちは。カエデです。
本日は正の数と負の数の
除法について勉強していきます。
除法ってなに?
と思った方、安心してください。
除法とは、「わり算」のことです。
そして、乗法(かけ算)と
ルールはほとんど同じです。
乗法の計算も振り返りながら
一緒に勉強していきましょう。
今日の勉強はこんな人におススメ!
・除法って何かわからない。
・わり算はできるけど符号で間違えちゃう
・分数の計算がわからない
・定期テストで50点以上目指したい!
1つでも当てはまった人は
ぜひ最後までいっしょに
勉強していってください!
除法ってなに?
除法とは、先ほども言った通り
わり算のことです。
わり算をしたその結果を
「商」といいます。
これも覚えておきましょう!
「〇〇の商を答えなさい。」
という問題も出てきますから!
除法の計算は
「符号の計算」「数字の計算」
で分けて計算してあげますよ!
数字の計算は暗算できるなら
そのままやっちゃいましょう!
割り切れない・・・
そんな問題は逆数を使います。
符号の計算
中学生の計算問題は
符号の計算と数字の計算を
分けて行いましょう。
符号の計算は
乗法と全く同じです。
乗法の符号の計算はこうでしたね。
(+)×(+)=(+)
(+)×(-)=(-)
(-)×(+)=(-)
(-)×(-)=(+)
(-)が奇数個なら答えは(-)
偶数個なら答えは(+)
除法もこれと同じなのです。
(+)÷(+)=(+)
(+)÷(-)=(-)
(-)÷(+)=(-)
(-)÷(-)=(+)
(-)が奇数個なら答えは(-)
偶数個なら答えは(+)
なぜ、除法と乗法は同じになるのか?
について説明していきます。
逆数
逆数って小学校のときに
勉強したことを覚えていますか?
どのような数にも必ず逆数
となるペアがあるのです。
分数の逆数にする
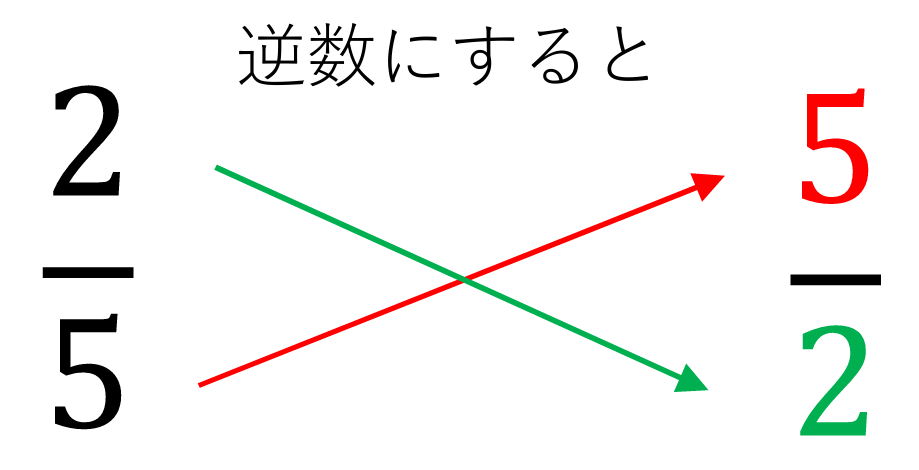
こんなやつです。
逆数とは、簡単に言うと
分母と分子をいれかえた数です。
もう少し数学的な言い方にすると
「かけて1になる数」となりますね。
\(\displaystyle \frac{2}{5} \)の逆数は\(\displaystyle \frac{5}{2} \)
\(\displaystyle \frac{5}{2} \)の逆数は\(\displaystyle \frac{2}{5} \)
\(\displaystyle \frac{2}{5} \)と\(\displaystyle \frac{5}{2} \)は逆数のペアなんです!
整数を逆数にする
整数であれば、分母を「1」と考えて
逆数にすることができます。
\(\displaystyle 4\) = \(\displaystyle \frac{4}{1} \) → \(\displaystyle \frac{1}{4} \)
小数を逆数にする
分数や整数と同じように
小数も逆数にすることができます。
小数は、分数になおして
その後逆数にするのです。
このとき、約分を忘れないように!
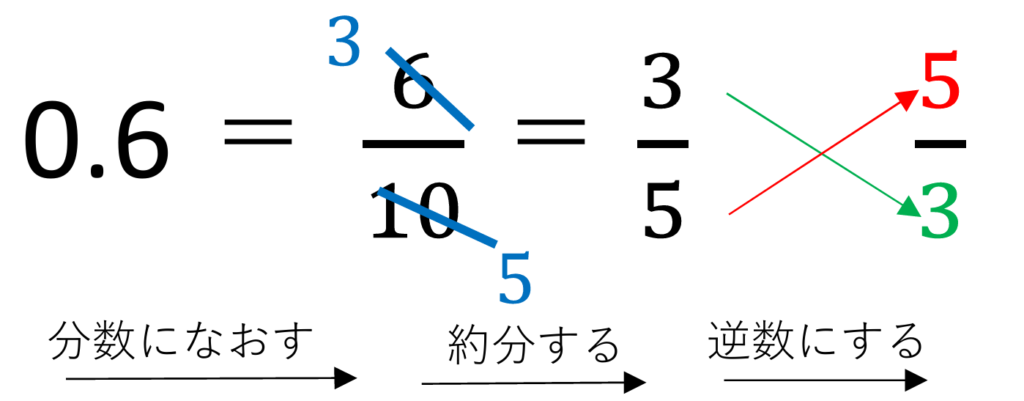
分数・整数・小数のどれでも
約分できるようにしましょう!
負の数を逆数にする
実は、負の数でも逆数に
することができるのです!
逆数は、
「分母と分子をいれかえた数」
でしたね!
では、\(\displaystyle -\frac{8}{3} \)を逆数にすると?
\(\displaystyle -\frac{3}{8} \) となります。
分母の\(\displaystyle 8\)と分子の\(\displaystyle 3\)を
いれかえると\(\displaystyle -\frac{3}{8} \)になりますね。
負の数であっても、符号はそのままで
分母と分子をいれかえるだけでOK!
逆数を用いた計算
わり算の計算のとき、
わる数を逆数にして
かけ算になおして計算する。
と勉強したことを覚えていますか?
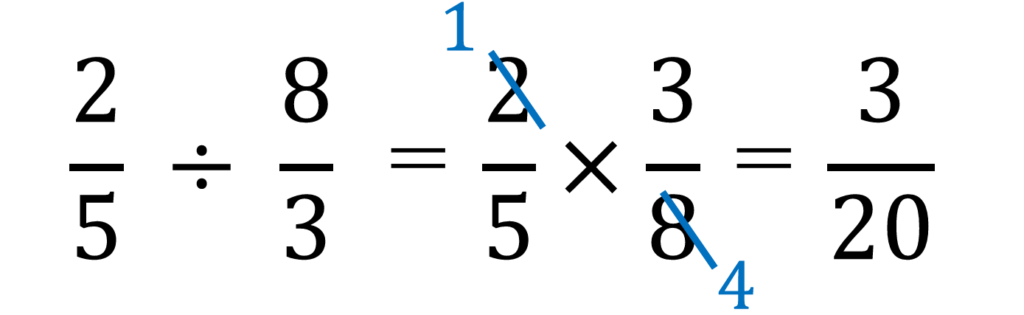
このように、かけ算になおして
計算することができましたね。
実は、今学習している負の数でも
同じように計算ができるのです!
正の数と負の数の除法
本番です!計算問題も解説していきます。
例題:次の計算をしましょう。
①\(\displaystyle -20\)÷\(\displaystyle 4\) ②\(\displaystyle -\frac{5}{8} \)÷\(\displaystyle (-\frac{15}{8}) \) ③\(\displaystyle 8\)÷\(\displaystyle (-6)\)
除法(わり算)の計算は
「符号の計算」と「数字の計算」で
分けて行うのでしたね!
①\(\displaystyle -20\)÷\(\displaystyle 4\)
符号は(-)÷(+)なので
答えの符号は(-)になります。
あとは数字の計算をするだけ!
わり算を暗算でできる問題は
頭の中でやっちゃってOK!
\(\displaystyle -20\)÷\(\displaystyle 4\)
=\(\displaystyle -(20÷4)\)
=\(\displaystyle -5\)
\(\displaystyle 20÷4\)と(-)÷(+)を
別々に計算してあげましょう。
②\(\displaystyle -\frac{5}{8} \)÷\(\displaystyle (-\frac{15}{8}) \)
=\(\displaystyle +(\frac{5}{8} \)×\(\displaystyle \frac{8}{15} \))
=\(\displaystyle \frac{1}{3} \)
(-)÷(-)=(+)
\(\displaystyle -\frac{5}{8} \)÷\(\displaystyle (-\frac{15}{8}) \)=\(\displaystyle \frac{1}{3} \)
それぞれ計算してくださいね。
最初に符号を計算して前に出しておくと
ミスをしにくいでのでおススメです!
③\(\displaystyle 8\)÷\(\displaystyle (-6)\)
=\(\displaystyle -(8\)×\(\displaystyle \frac{1}{6}) \)
=\(\displaystyle -\frac{4}{3} \)
見ているだけで計算ができるように
なる訳ではありませんからね?
自分で解いてみることが大切です!
練習問題
まとめ
正の数と負の数の除法について
少しでも理解が深まりましたか?
「除法」とはわり算のこと
「商」はわり算の結果のことでしたね!
計算の仕方は
1.符号の計算
2.数字の計算
この2つが必要です。
1の符号の計算はこう!
(+)÷(+)=(+)
(+)÷(-)=(-)
(-)÷(+)=(-)
(-)÷(-)=(+)
(-)が奇数個なら答えは(-)
偶数個なら答えは(+)
2の数字の計算は
頭の中でわり算ができるなら
そのまま計算しちゃって!
できないなら逆数にしてかけ算で計算!
・逆数は分母と分子をいれかえる
・符号はどのままで変えない
この2つを覚えておきましょう!



コメント