こんにちは。カエデです。
中学校に向けての勉強をするために、必要なこと。
小学校のテストとは違い、中学校のテストは範囲も広く難易度も高いです。
でも、大丈夫!
このサイトであなたが定期テストで50点以上取ることができるように
わかりやすく解説していきます。
●勉強が苦手だなー。
●中学生になってから何を言っているかさっぱり( ;∀;)
●学校1日休んだだけなのに、この前と全然違うことやってる。。。
●学校の先生の声が小さくて全然聞こえない。
こんな人が本当にたくさんいます。
私は大学を卒業後、10年間「家庭教師」として合計150名以上の生徒に勉強を教えてきました。
今でも現役ですが、勉強が苦手な人が少しでもできることが増えるようにと思いみなさまに、
勉強のコツをお届けしていきます。
では、さっそく始めていきましょう!
今回のキーワードはこちら!
正の数・・・数字に「+(プラス)」がつくもの
負の数・・・数字に「−(マイナス)」がつくもの
例外 ・・・「0」は正の数でも負の数でもない数
整数 ・・・分数や小数を使わなくても表せる数
自然数・・・正の数でなおかつ整数であるもの
正の数・負の数とは
正の数・負の数という言葉を初めて聞く人もいるとおもいます。まずは、言葉の意味を説明していきますね。
正の数とは、小学生の算数で学習してきたものがすべて「正の数」といいます。
正の数は「+3」「+17」などと今まで習ってきたものに「+(プラス)」がつくだけ。
負の数は、+ではなく「ー(マイナス)」で表す数のことです。
気温で-1℃とか聞いたことありますか?
あれって0℃を基準にしてそれよりも低くなると-1℃とか-7℃とかって表すんですよ。
この「基準」からという考え方がとても大事です!
ただ、ここで例外が1つだけあります。
それは、「0」です。
ゼロは正の数にも、負の数にも含まれません。
なので、中学生の数学で習うものは
・正の数
・負の数
・0
この3つですべてが表されるのです。
基準って何?
ものごとを数字で表すときって、基準があるんですよ。この基準を見つけることが大事!!
例えば先ほどの「0℃」っていう基準は、
「水が氷になる時の温度を0℃とする」という基準があるのです。
3℃→基準の0℃よりも3℃高いので「+3℃」
-1℃→基準の0℃よりも1℃低いので「-1℃」
実は、それとは別に絶対温度というものがあります。
絶対温度(単位:K)とはどんなものでも動くことができなくなってしまう温度のことです。
それを基準としたら
絶対温度が0Kを基準としたとき、
先ほどの温度は「+273K」と表すのです!
※覚える必要ないです笑
他にも、
富士山の高さは3776mだ。
これは実は日本(東京湾)の海面を基準の「0m」としてそこから「+3776m」ということになります。
あとは、
自分の家から学校までの道のりは800mだ。
としたら、自分の家が基準の0mとなります。
学校の位置は+800mとするわけですね。
また、逆方向の500m駅があるとすると、駅の位置は負の向きにあるので「-500m」となるのです。
整数・自然数って何?
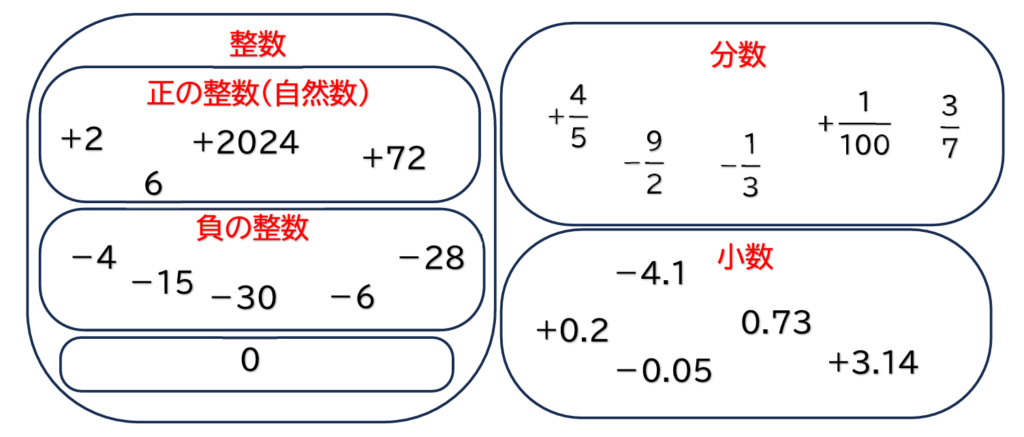
中学1年生で習うものは上の表の通りです。
では、一つずつ説明していきましょう。
①小数
小数とは、より小さい数を表すため細かくしたときの間の数です。
1を10こに分けたうちの1こ分を0.1
1を100こに分けたうちの1こ分を0.01
と表します。
小数で表すときは小数点「.」を使うので、小数点が目印になりますね。
では、こちらの数直線ではどうでしょう?
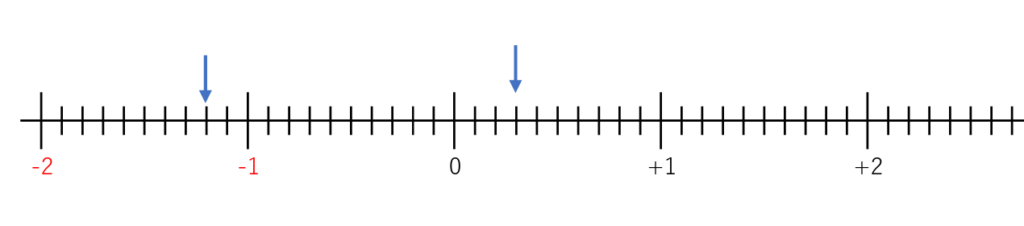
2つの矢印について考えていきましょう。
まず、この数直線の最小めもりはいくつでしょうか?
0から+1まで10個に分けられているので、小さいめもりが「0.1」となります。
1を10こにわけたうちの1こ分が0.1です。
右側の矢印は「0」と「1」の間にありますね。

わかった!
めもりが3つ右に進んでいるから答えは
「0.3」だ!

その通り!
では、数直線で確認していきましょう。
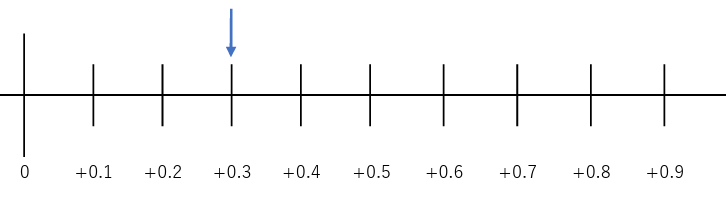
1めもりで「0.1」ということは右側に3めもりで、答えは+0.3ということですよね。
このように正の数が大きくなる向きを「正の向き」
負の数が大きくなる向きを「負の向き」といいます。あわせて覚えておきましょう!
では、先ほどの左の数直線はどうでしょう?
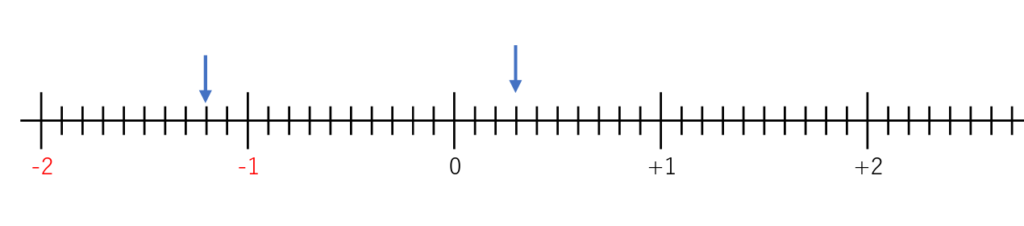

左の矢印は、どちらの向きに進んでいるでしょう?
正解は、「負の向き」に進んでいます!
※左側に進む=負の向きに進む ことが多いです。
では、どれだけ進んでいるか見ていきましょう!
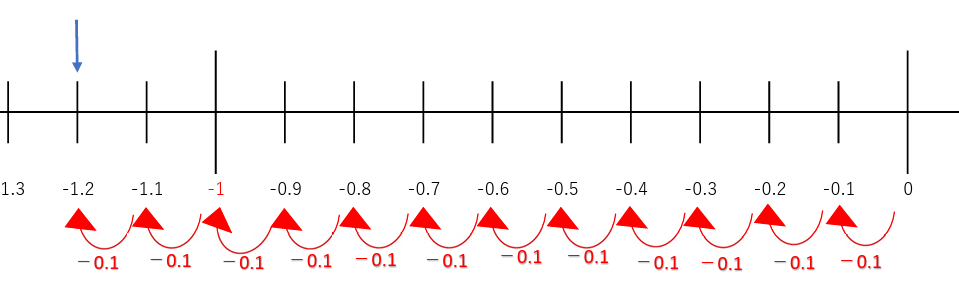
少し見づらいですかね(汗
今回の矢印は、-1と-2の間にあるので、-1からどれだけ進んだかを考えてあげればよいですね。
「-1から負の向きに2めもり分進む」ことになります。
今回は負の向きなので1めもりで「―0.1」、2めもりで「-0.2」進むことになります。
なので、―1から―0.2進んだ先の答えは、
―1.2となります。

カエデ先生、小数があれば分数っていらないんじゃないの?

いい質問ですね。
じゃあ、分数も必要な理由について説明しよう!
②分数
分数も小数とそこまで大差はありません。
1をいくつかに分けたもので表すことができます。
分数は、1をいくつかに分けた数を分母、そのうちの使う分を分子とこのように表します。
たとえば、0.1=\(\frac{1}{10}\) 0.4=\(\frac{2}{5}\)
などと表すことができるのです。
ただし、
小数では表せないものも存在します。
例えば\(\frac{1}{3}\)
これは、先ほどの割り算をしても
1÷3=0.333333333333333333
となってしまうため、確実な数を表すには分数を使うしかありません。
なので、1÷3=\(\frac{1}{3}\)とするのです。
どうですか?こっちの方が簡単じゃないですか!?
逆に、小数はすべて分数で表すことができます。
中学の数学では、小数よりも分数を使う機会が圧倒的に多いです!
なので、今のうちに分数で表せるようにしておきましょう。
③整数
つづいて、整数とは何?ということについてです。
整数とは、分数・小数以外のもの全てです。
終わり。
って終わられると困りますよね。笑
もう少し詳しく説明をすると、整数は分数や少数を使わなくても表せる数で
大きく分けて3種類あります。
それは、
・正の整数
・負の整数
・0
の3つです。
コチラの数直線を見てください。
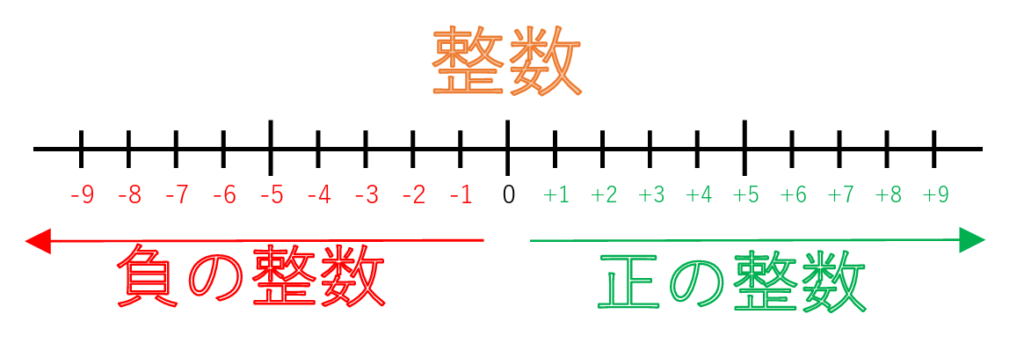


これ、ぜんぶ整数です。
正の整数・負の正数は無限にあります。
ですが、0はもちろん1つですね。
正の整数は「+」を使って表せる整数。
負の整数は「-」を使って表わせる整数のことです。
④自然数
自然数 = 正の整数です。
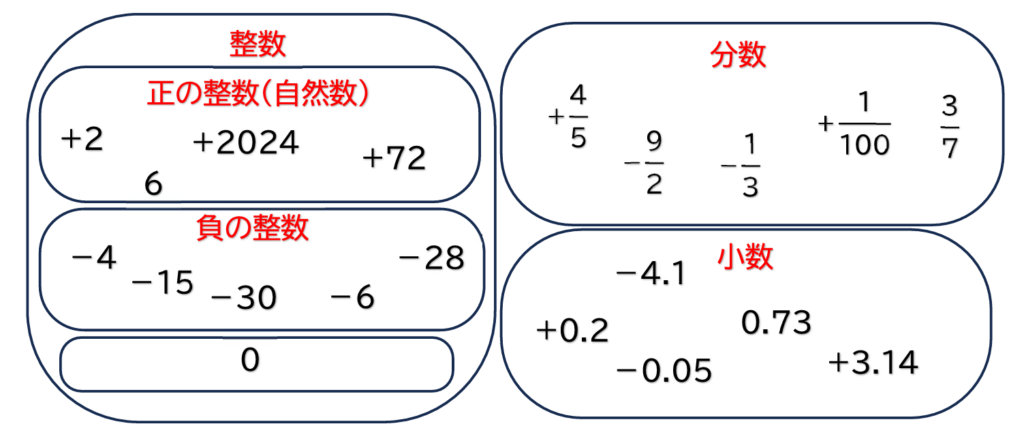
初めに見たこの画像を見て気づいていた方は鋭いですね!
これからは負の数を使った問題もたくさん出てくるので今のうちに完璧にしておきましょう!
まとめ
本日は正の数と負の数についてお話をしてきました。
皆さんは何となくわかりましたか?
正の数とは・・・「+」を使って表す数のこと
負の数とは・・・「-」を使って表す数のこと
※0は正の数でも負の数でもない!
整数は、 正の整数 負の整数 0 の3種類
中学の数学では小数よりも分数を使うことのほうが多い。
覚えたことは必ず復習することが大切ですよ!!!



コメント