学校には行けない、、、でも勉強はしなきゃいけないのはわかっている。
けど、、、勉強したいけど何から始めていいかわからない。。。
まずこう考えてこのブログを見ているあなたは本当に偉いです。自分でなんとかしたいと考えている方のためにこのスタディブログを作成しております。
そんな中学生向けの1回10分の勉強法を載せていきます。「何を勉強したらいいのか?」「自分でやっても何がなんだかわからない」と躓いてしまっているあなた!
ここでは無料で何をやればよいかの解説、練習問題を含め1つの講義を10分程度で行えるようにしています。
これを毎日やって苦手を克服していきましょう!
※基礎を固めるための内容になっているので、定期テストで80点以上を目指したい人向けではありません。
10年間家庭教師として50名ほどの学校に行くことができない生徒の勉強に携わり、自ら進んで学校に行くことができるようになりました。そうした指導を行ってきました私から、そんな不登校の生徒様に向け、勉強のノウハウをお伝えしていこうと思いますので、ぜひご覧ください!
本日の勉強内容
本日の学習内容はこちらになります。
- 前回の復習 → 直線の式・一次関数の式とは?
- 一次関数のグラフを書くために必要なこと【3選】
- グラフを書くための手順
- 実際にグラフを書いてみよう!
ここまででおよそ10分。
本日も頑張りましょう!!
前回の復習 直線の式、一次関数の式とは?
まずは前回の復習からです。一度学習したことをもう一度振り返り、「うんうん、大丈夫覚えてる」と感じることで、より自分の力にすることができますからね。
結論は
直線の式=一次関数の式= \(\displaystyle y=ax+b\) です。
すべて同じことを表しているんですね。
その中でも「\(\displaystyle a\)」のことを傾き(変化の割合)、「\(\displaystyle b\)」のことを切片といいました。
一次関数の傾きは、\(\displaystyle x\)の値が1増えると\(\displaystyle y\)の値がいくつ増えるかを表していましたね。
一次関数の切片は、\(\displaystyle x\)の値が0のとき\(\displaystyle y\)がいくつなのか?を表していました。
そのため、 \(\displaystyle y=-2x+3\) という一次関数の式では
\(\displaystyle a\)(傾き)=-2 なので \(\displaystyle x\)の値が1増えると\(\displaystyle y\)の値が -2増えることがわかります。
\(\displaystyle b\)(切片)=3 なので \(\displaystyle x\)の値が0のとき\(\displaystyle y\)が 3 になるということです。
どうですか?覚えていましたか?
覚えていなかったという方は、本日は前のページに戻りもう一度復習しましょう。
焦らず自分のペースで進んでいくことが大切ですよ。
では次に、前の内容がわかっていたという皆さんに問題です!
問題 一次関数 \(\displaystyle y=5x-4\) について次の2つの問題に答えましょう。
(1) 傾きはいくつですか?
(2) \(\displaystyle x\)が 2 増えるとき、\(\displaystyle y\)はいくつ増えますか?
いかがでしょうか?答えは、、、
(1) 5
→\(\displaystyle y=ax+b\)の「\(\displaystyle a\)」が傾きにあたるので、\(\displaystyle y=5x-4\) の「5」が答えとなります。
(2) 10
→a(傾き)は「5」なので、\(\displaystyle x\)が1増えたとき\(\displaystyle y\)は「5」増えます。
ということは\(\displaystyle x\)が2増えたときは、その2倍で10増えるということです。
皆さん理解できましたか?
復習はここまでにして次に進みましょう!
一次関数のグラフを書くために必要なこと【3選】
ここでは一次関数のグラフを書くために必要な3つのことについて理解してもらいます。
- 一次関数の式は直線で書こう!
なんだ、そんな当たり前のことか。。。
と思うかもしれませんが、中学では関数のグラフが3種類出てきます。
①直線のグラフ ②双曲線のグラフ ③放物線のグラフ
※双曲線のグラフについては1年生の反比例、放物線については3年生の関数\(\displaystyle y=ax²\)の単元で詳しく学習します。
そのため、一次関数 \(\displaystyle y=ax+b\) のグラフと聞くと直線だ!
とその瞬間に理解できるようにしましょう。 - グラフのスタートは\(\displaystyle b\)(切片)から!
グラフを書くときはまず\(\displaystyle b\)(切片)の点を取るために\(\displaystyle y\)軸からスタートします。
例えば、\(\displaystyle y=3x-2\)の場合は以下のように考えましょう。
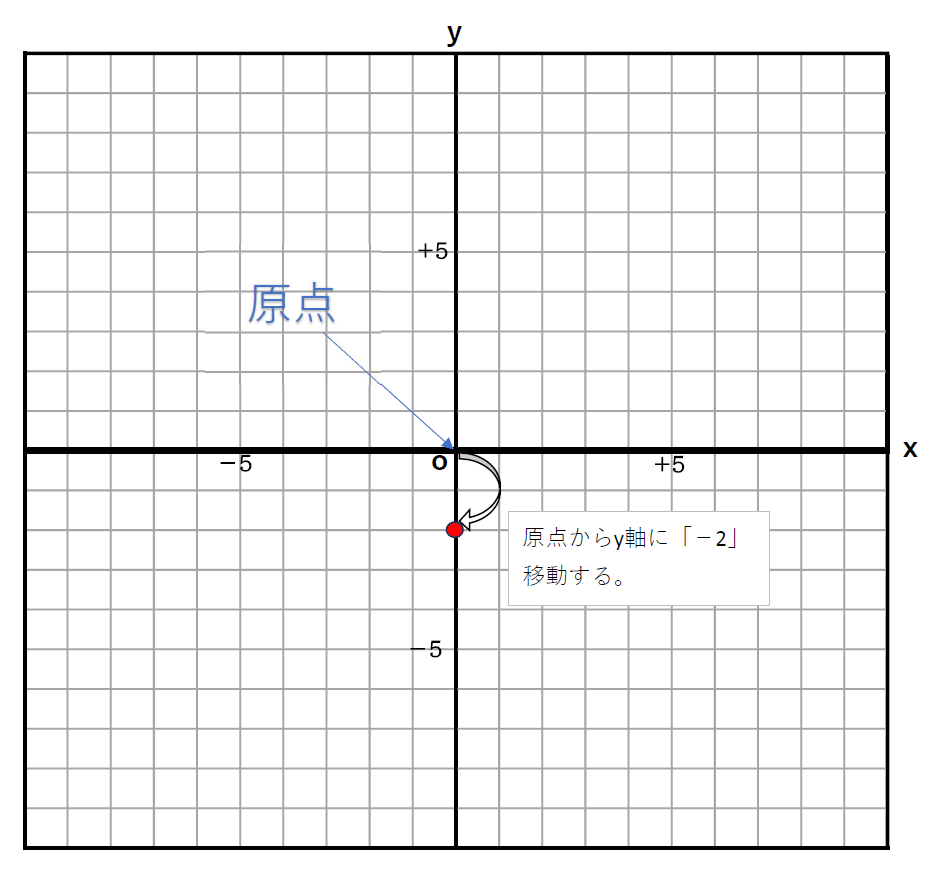
このように、\(\displaystyle b\)(切片)に合わせて上下に動かし、スタート地点を決めてあげます。
3.\(\displaystyle a\)は分数で考えよう!
\(\displaystyle a\)(傾き)は分数で考えましょう。
グラフを書くときは上の式を \(\displaystyle y=\frac{□}{△}x+b\) と考えます。
こんな感じで、作り直した式を〇で囲んであげてください。
丸で囲まれた部分が移動する値になります。
1つ目の\(\displaystyle y=3x-2\) は\(\displaystyle x\)に「1」、\(\displaystyle y\)に「3」進みます。
2つ目の\(\displaystyle y=\frac{2}{3}x+1\)は\(\displaystyle x\)に「3」、\(\displaystyle y\)に「-2」進みます。
分数に表すことでどのように移動するかを目で見ることができるので、分数にすることでミスを減らすことができます。
グラフを書くための手順
グラフを書くための手順は大きく分けて4つあります。
① \(\displaystyle y=\frac{□}{△}x+b\)のグラフに書き換える。
② \(\displaystyle b\)(切片)のスタート地点に点を打つ。
③ スタート地点から、\(\displaystyle x\)に△、\(\displaystyle y\)に□進んだところに点を打つ。(これを何回かやったほうがきれいなグラフになります)
④ 打った点を通るように定規で線を引く。(グラフの端から端まで線を引きましょう!)
実際に例題をやってみます。
ぜひあなたもご一緒に!
例題) \(\displaystyle y=2x+1\)のグラフを書きましょう。
解き方
① \(\displaystyle y=\frac{□}{△}x+b\)のグラフに書き換える。
→\(\displaystyle y=\frac{2}{1}x+1\)
このときに斜めに〇を囲んでおきましょう。
② \(\displaystyle b\)(切片)のスタート地点に点を打つ。
→原点からy軸を「1」移動
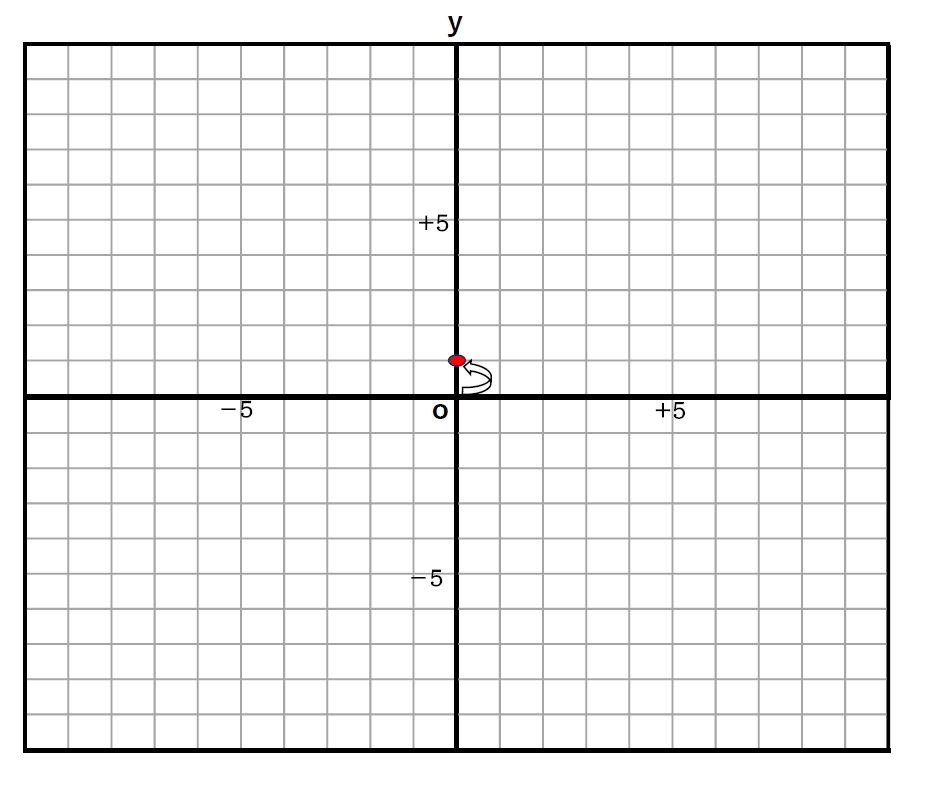
③ スタート地点から、\(\displaystyle x\)に△、\(\displaystyle y\)に□進んだところに点を打つ。(これを何回かやったほうがきれいなグラフになります)
→\(\displaystyle y=\frac{2}{1}x+1\)なので、\(\displaystyle x\)に「1」、\(\displaystyle y\)に「2」進む。
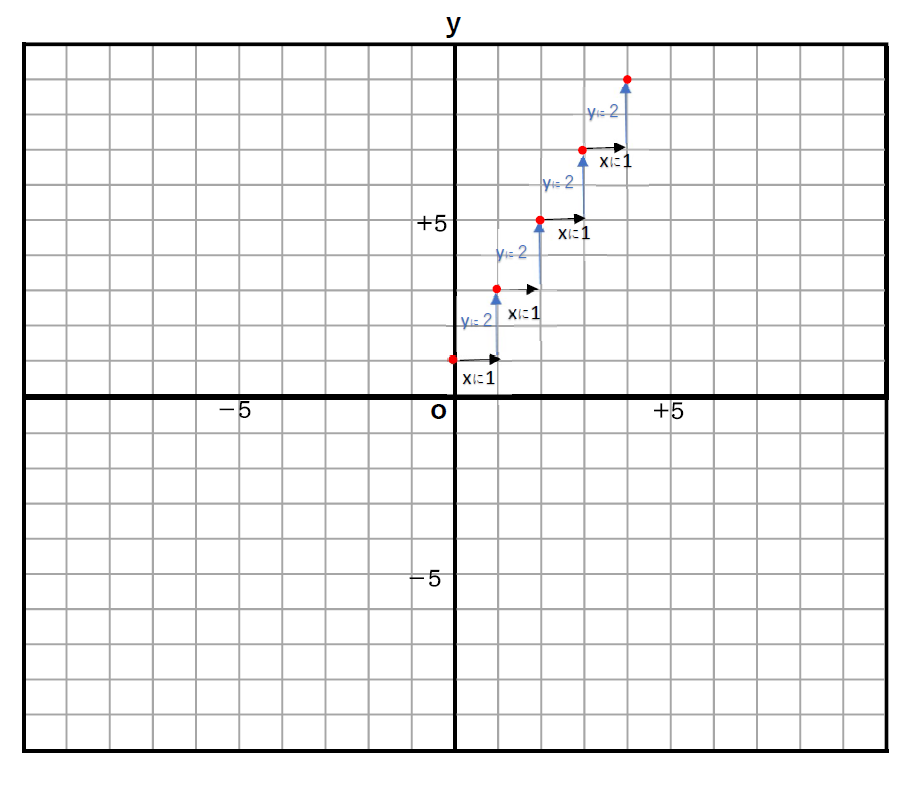
④ 打った点を通るように定規で線を引く。(グラフの端から端まで線を引きましょう!)
→グラフの端から端まで線を引くだけ!!
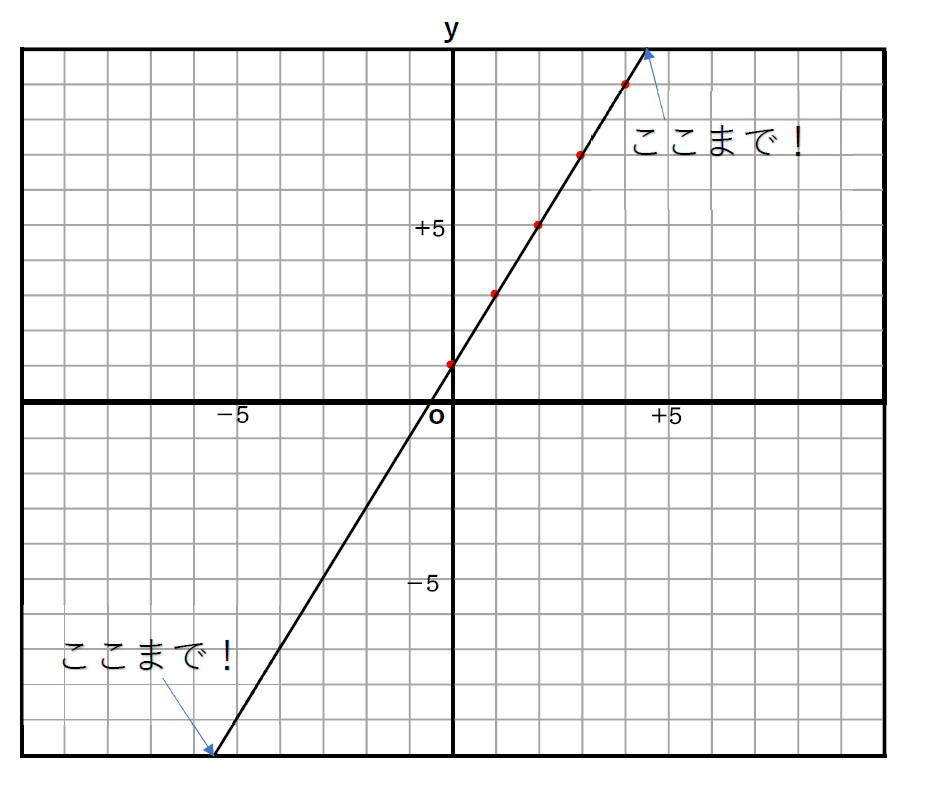
理解できましたか?
理解できるまで何度も見返すことが大切です!(10分超えてしまいますが、、、)
実際にグラフを書いてみよう!
ここからは練習問題です。
プリントできる方は印刷してやってみてください!!
☆練習問題:グラフを書いてみよう
グラフを書いてみよう〈解答〉
皆さんはできましたか?
手順通りにやれば難しくないはずです!
マスター出来たら次の授業へ進みましょう!!
≫≫一次関数の式の求め方①グラフから式を求める問題

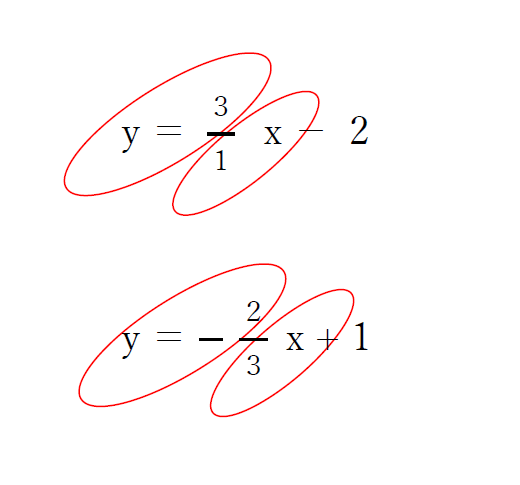

コメント