こんにちは。カエデです。
先日、生徒から質問があった問題です。
こんな問題、みたことありますか?
横の長さが、縦の長さよりも4cm長い
長方形の紙があります。その紙の四隅から
2㎝正方形を切り取って上が開いている
直方体の容器をつくると容積が64㎝³でした。この紙の縦の長さは何㎝ですか?
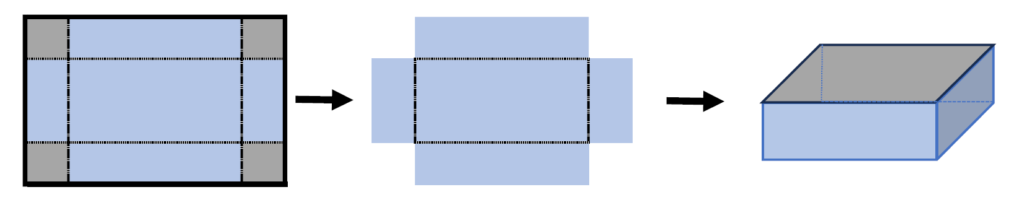
本日はこの問題の解き方について勉強していきましょう。
どこが\(\displaystyle x\)?
方程式の文章題では、知りたいものを
\(\displaystyle x\)と置きます。
今回の問題は、
横の長さが、縦の長さよりも4cm長い
長方形の紙があります。その紙の四隅から
2㎝正方形を切り取って上が開いている
直方体の容器をつくると容積が64㎝³でした。この紙の縦の長さは何㎝ですか?
この問題で知りたいのは、
縦の長さなので、
縦の長さ→\(\displaystyle x\)㎝です。
必要な長さを見つけよう
横の長さが、縦の長さよりも4cm長い
長方形の紙があります。その紙の四隅から
2㎝正方形を切り取って上が開いている
直方体の容器をつくると容積が64㎝³でした。この紙の縦の長さは何㎝ですか?
縦の長さが\(\displaystyle x\)㎝で、
横の長さが縦の長さよりも4cm長いので、
横の長さは\(\displaystyle x\)㎝よりも4㎝長いことから
横の長さ→(\(\displaystyle x+4\))㎝
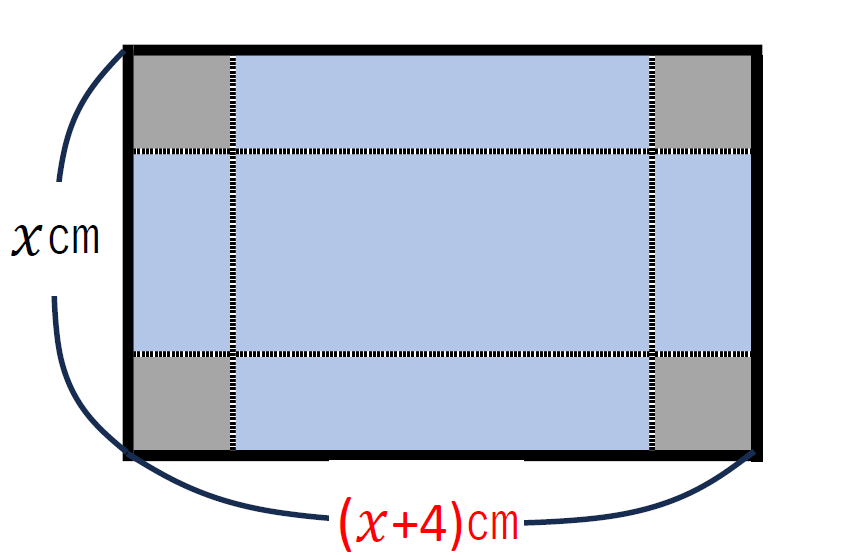
四隅から2㎝正方形を切り取って
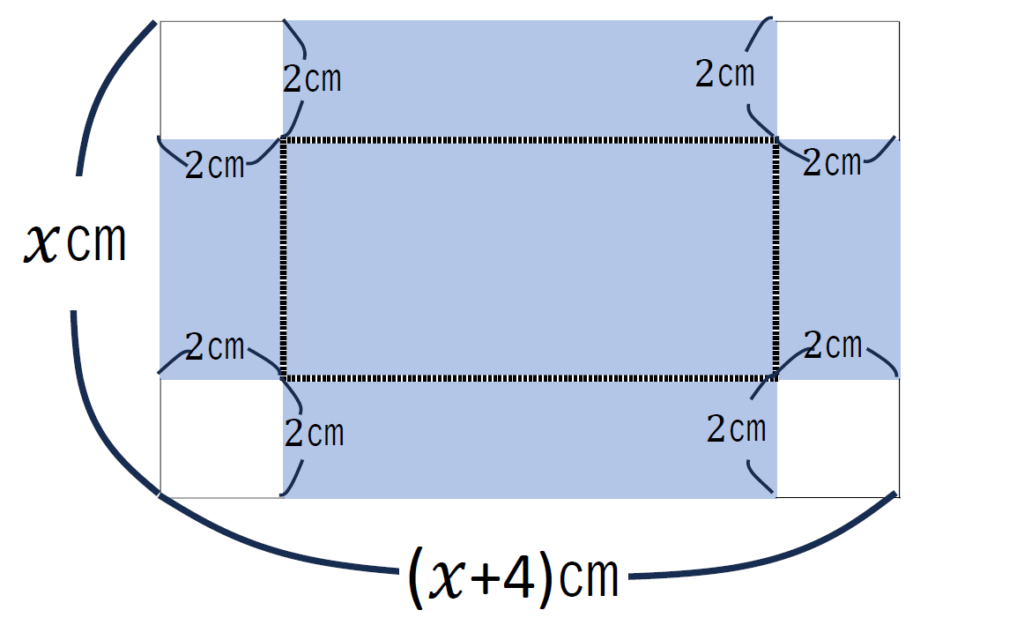
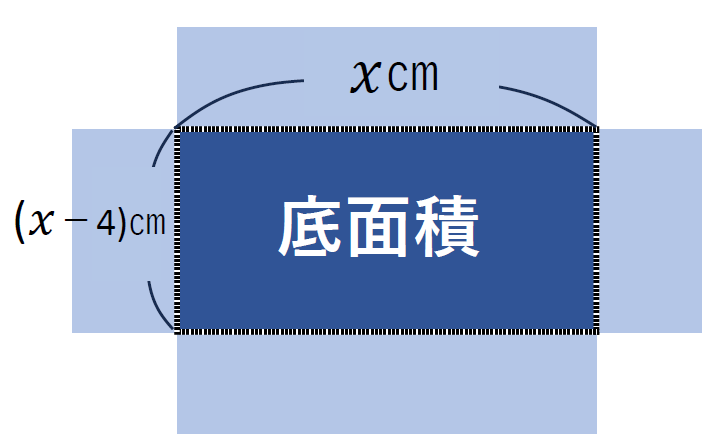
底面積を求める
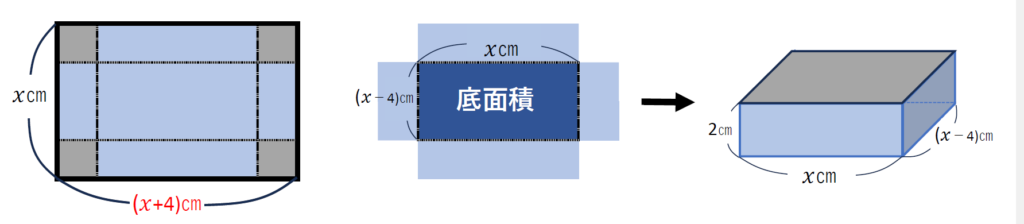
底面積の場所は覚えておきましょう。
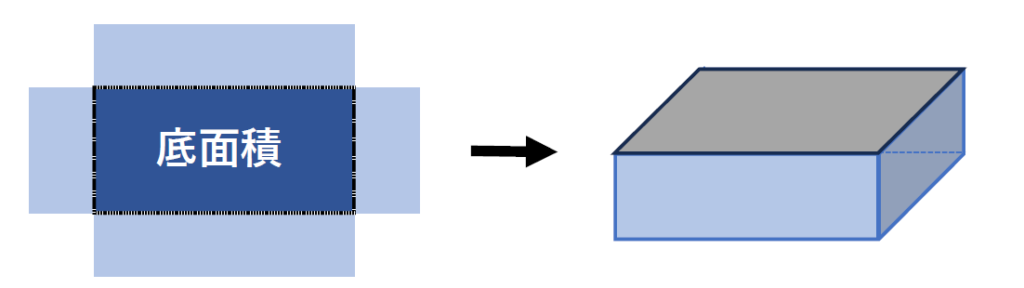
では、底面積の縦と横の長さは?
四隅から2㎝ずつ短くなったので、
縦も横も4㎝短くなり、以下のようになります。
縦の長さ=\(\displaystyle x-2-2\)=(\(\displaystyle x-4\))㎝
横の長さ=\(\displaystyle (x+4)-2-2\)=\(\displaystyle x\)㎝
直方体の容器をつくると
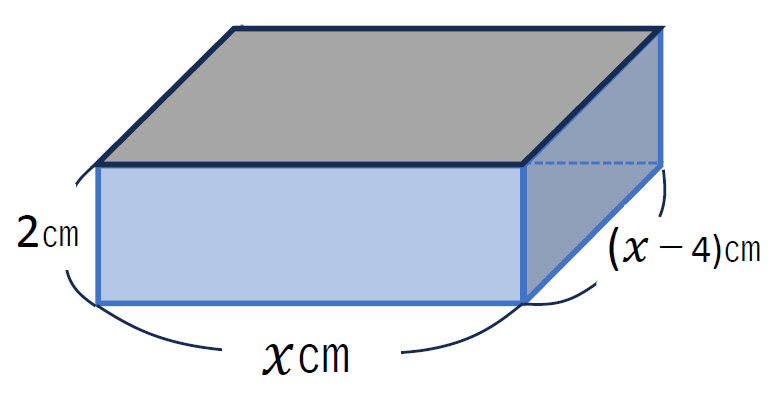
ここまでの流れはすぐにイメージ
できるようにしておきましょう。
容積を求める
横の長さが、縦の長さよりも4cm長い
長方形の紙があります。その紙の四隅から
2㎝正方形を切り取って上が開いている
直方体の容器をつくると容積が64㎝³でした。この紙の縦の長さは何㎝ですか?
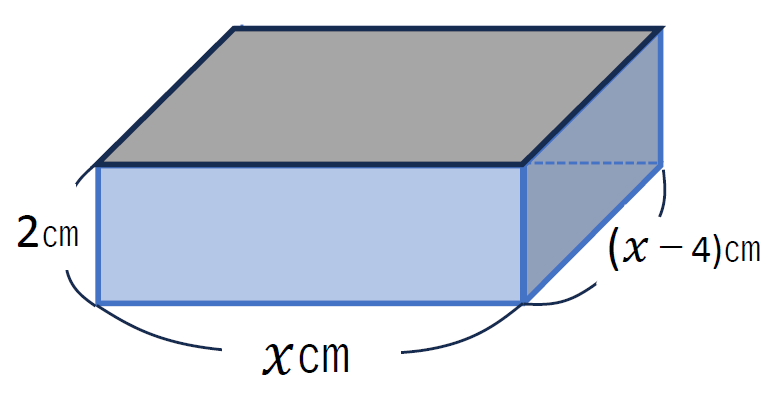
直方体の容積(体積)の求め方は
底面積×高さ です。
そのことを踏まえて方程式をつくると
(\(\displaystyle x-4\))×\(\displaystyle x\)×\(\displaystyle 2\)=\(\displaystyle 64\)
整理すると
\(\displaystyle 2x(x-4)\)=\(\displaystyle 64\)
展開して( )を外す
\(\displaystyle 2x²-8x\)=\(\displaystyle 64\)
左辺に移行する
\(\displaystyle 2x²-8x-64\)=0
両辺を2で割る
\(\displaystyle x²-4x-32\)=0
因数分解する
\(\displaystyle (x-8)(x+4)\)=0
\(\displaystyle x\)=8,\(\displaystyle x\)=-4
答えの前の注意点
\(\displaystyle x\)=8,\(\displaystyle x\)=-4 なので
A. 8㎝、-4㎝
とはなりません!
答えが-4㎝?とはなりませんよね?
存在しない答えの場合は、この言葉をつけましょう。
\(\displaystyle x\)=○○ は不適切なので →(答え)
このように、答えが不適切でないか?
を確認してあげる必要があります。
正の数・自然数のみが答えになるものが
多いですが必ず問題文を確認してください。
そのため、長方形の紙の縦の長さは
A. 8㎝
のみとなります。
これで容積を問われる二次方程式の利用は
ばっちりですね!!
まとめ
長方形の紙と直方体の問題は、
①直方体の底面をイメージする。
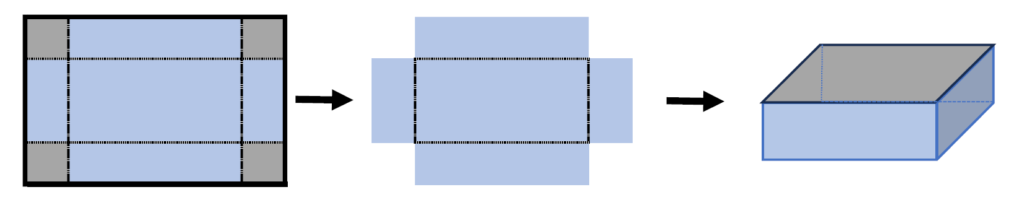
②どこが知りたい?知りたい箇所を\(\displaystyle x\)とおく。
その他の長さも書き込むと見やすいですね。
③容積(体積)=底面積×高さ の公式に当てはめて
方程式の解を求める。
(\(\displaystyle x-4\))×\(\displaystyle x\)×\(\displaystyle 2\)=\(\displaystyle 64\)
④解は問題に適しているか?必ず
問題文をみてチェックする。
定期テストで同じ問題が
出たらラッキーですね♪



コメント