今回は、
一次関数の式の求め方
について解説していきます。
内容が長くなりそうなので、
2回に分けて行います。
1回目は
グラフから式を求める
問題について解説していきます。
この記事はこんな人におススメです!
・計算問題はできるけど、関数に入ってから全く分からない
・何日か学校休んでたら学校の授業についていけなくなってしまった
・定期テストで50点以上取りたい!
・学校の授業は聞いていても分からない
・学校に行っていないけど勉強はしたい!
そんな中学生向けの
1回10~15分の勉強法を
載せています。
問題の解き方の解説や傾向、
練習問題を含め
すべての講義を15分程度で
行えるようにしています。
これを毎日やって
定期テスト50点以上を目指しましょう!
※基礎を固めるための内容になっているので、
定期テストで80点・90点を目指したい
人向けではありません。
私は10年間家庭教師として
150名ほどの生徒、50名ほどの不登校の生徒の
勉強に携わり、指導を行ってきました。
そんなカエデが
不登校の生徒様・勉強が苦手な生徒様に向け、
勉強のノウハウをお伝えしていきます。
ぜひご覧ください!
一次関数のグラフから式を求める
まずはグラフがあるよ!
って問題から式を求めるパターンです。
これは、前回のグラフの書き方と
考え方は似ています。
手順は以下の3つ!
①切片(\(\displaystyle b\))の座標を見つける
まずは下のグラフの
切片の座標を見つけてみましょう。
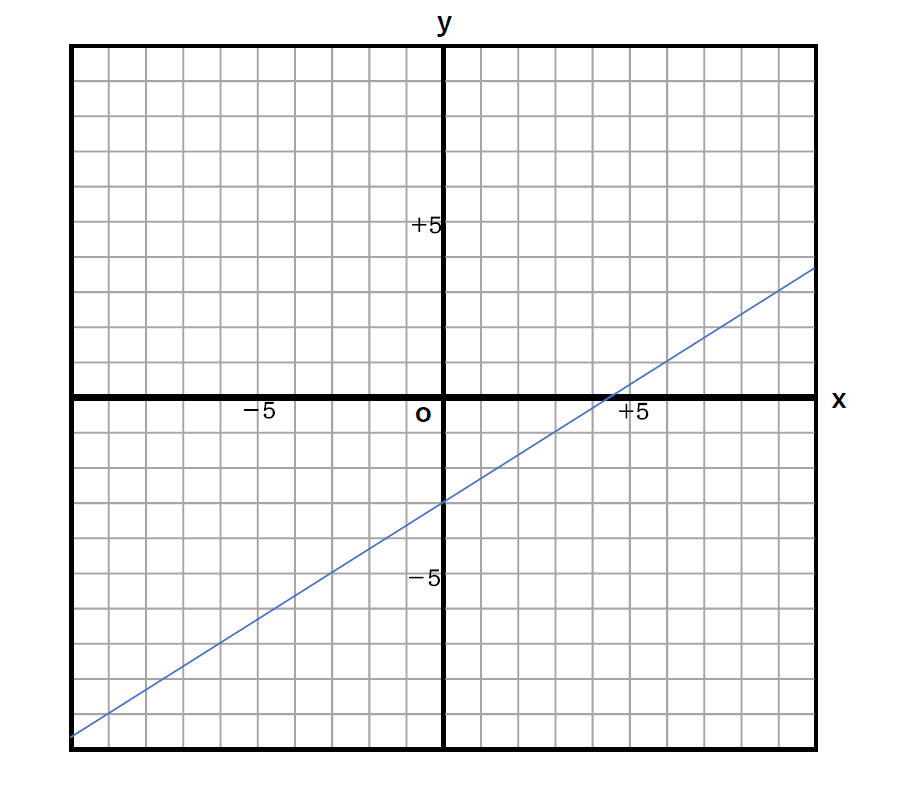
切片とはグラフにある
\(\displaystyle y\)軸上の数(\(\displaystyle x=0\)のときの\(\displaystyle y\)の値)です。
「原点から上下にどれくらい進んだか」
で見つけることができます。
上に進んだら「+」
下に進んだら「-」ですよ!

わかりましたか?

うん、切片は-3でしょ。

お、正解。
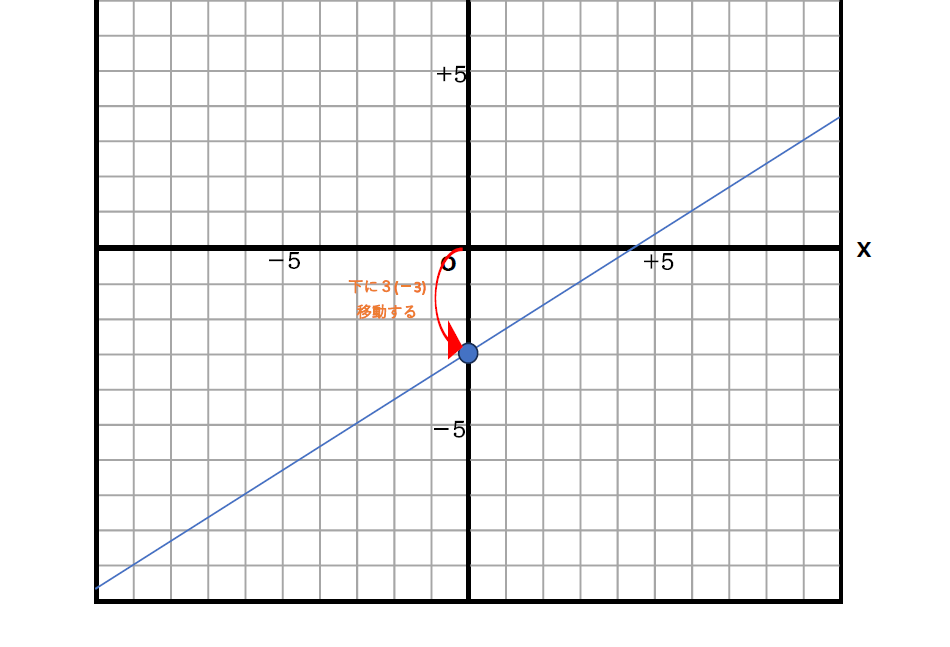
原点(0,0)から見て、
上に進んだら「+」
下に進んでいたら「−」になります。
このグラフでは
下に3マス分進んでいたので
切片は「-3」となります。
この時点で\(\displaystyle b\)がわかって、
式は\(\displaystyle y=ax-3\)
というところまでわかるのです。
これで半分終わりですね。

まじで、楽勝じゃん。

次は\(\displaystyle a\)の値を求めていきます。
\(\displaystyle a\)の値は少し難しいので頑張ってついてきてくださいね。

・・・・・。
②切片から右と上下に進んでピッタリの座標を見つける
では、次にグラフの切片から
進んで座標を見つけてみましょう。
グラフの右側から探すのがポイントですよ。
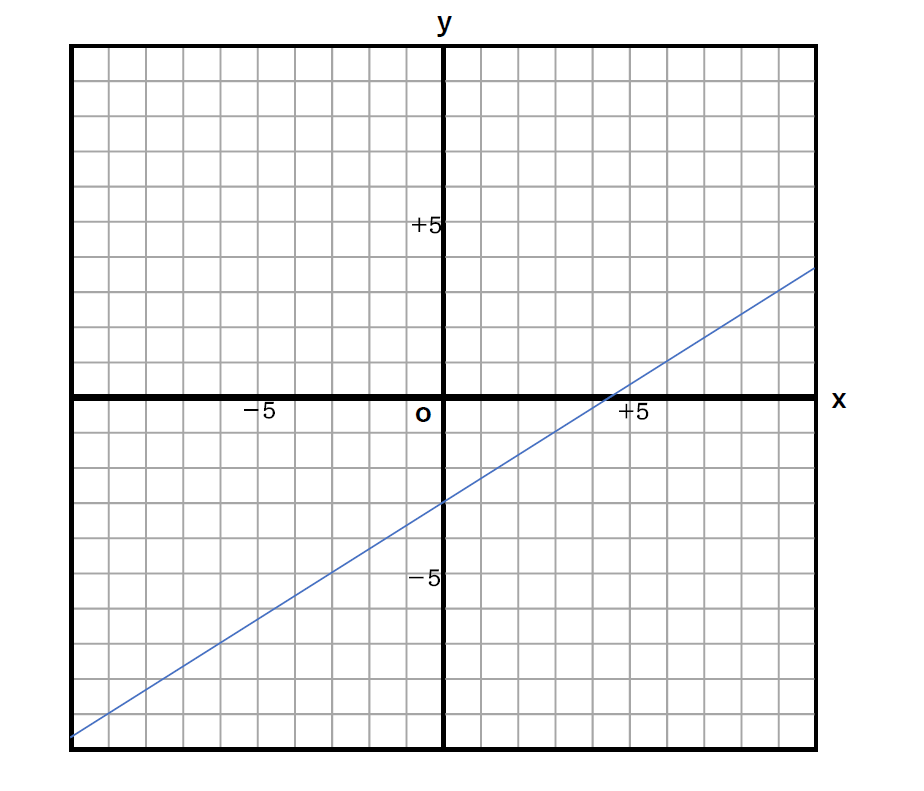

(3,-1)です。

え、はやっ!!もう見つけたの!?
待って。ちゃんと説明もするから。
座標とは、\(\displaystyle x\)と\(\displaystyle y\)
それぞれが示すそのときの値で、
右にいくほど\(\displaystyle x\)は大きく、
上にいくほど\(\displaystyle y\)の値は大きくなります。
座標を示すときは(\(\displaystyle x\)の値,\(\displaystyle y\)の値)と書きますよ。
今回Aさんが見つけてくれたのはココ。
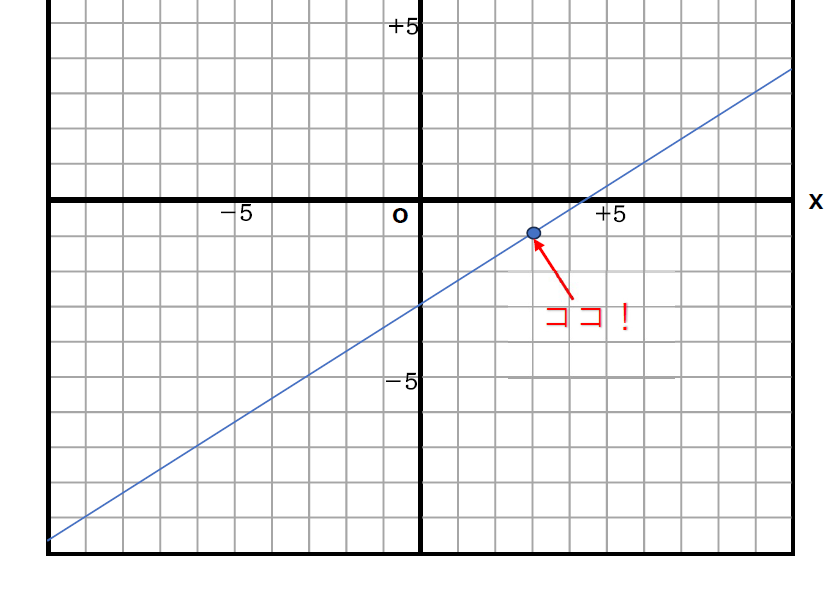
原点(0,0)からみて、
右に3進んで、
下に1進んでいます。
\(\displaystyle x\)は下に進んでいるときに「-」になるので注意しましょう。
その他にも
(6,1)や(9,3)も正解です。
※左側の座標は省いています。
③切片から上下(\(\displaystyle y\))に進んだ数を右(\(\displaystyle x\))に進んだ数で割る
次が最後になります。
頑張ってついてきてください!
上下(\(\displaystyle y\))に進んだ数÷右(\(\displaystyle x\))に進んだ数
ですね。
ここでも先ほどと同じように、
切片から\(\displaystyle y\)が上に進んだ場合は「+」、
下に進んだときは「-」となります。
上下に進んだ数のことを、
→\(\displaystyle y\)の増加量
右に進んだ数のことを、
→\(\displaystyle x\)の増加量といいます。
\(\displaystyle y\)の増加量÷\(\displaystyle x\)の増加量で
求めた値のことを変化の割合といいます。
これを式にすると
\(\displaystyle 変化の割合=\frac{yの増加量}{xの増加量}\)
となります。
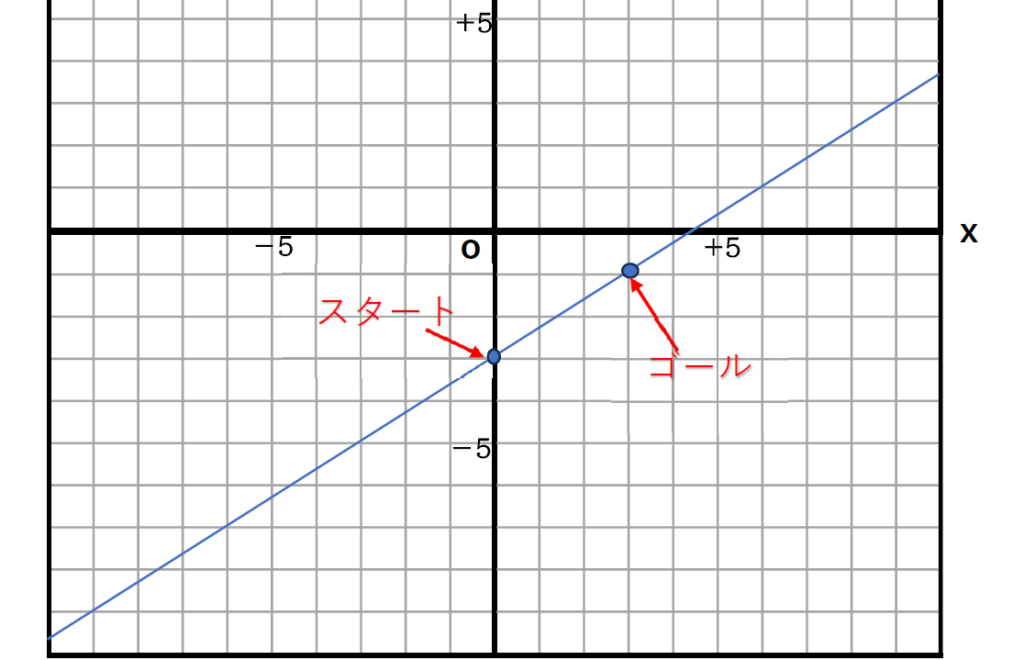
①と②で見つけた2つを使って進んだ値を調べていきましょう。
①では切片(\(\displaystyle b\))が-3
②では点(3,-1)を見つけました。
その2つを
①スタート
②ゴールとして
どれだけ進んだかを考えていきます。

カエデ先生、もう私わかっちゃった。

本当?じゃあ教えてもらえますか?
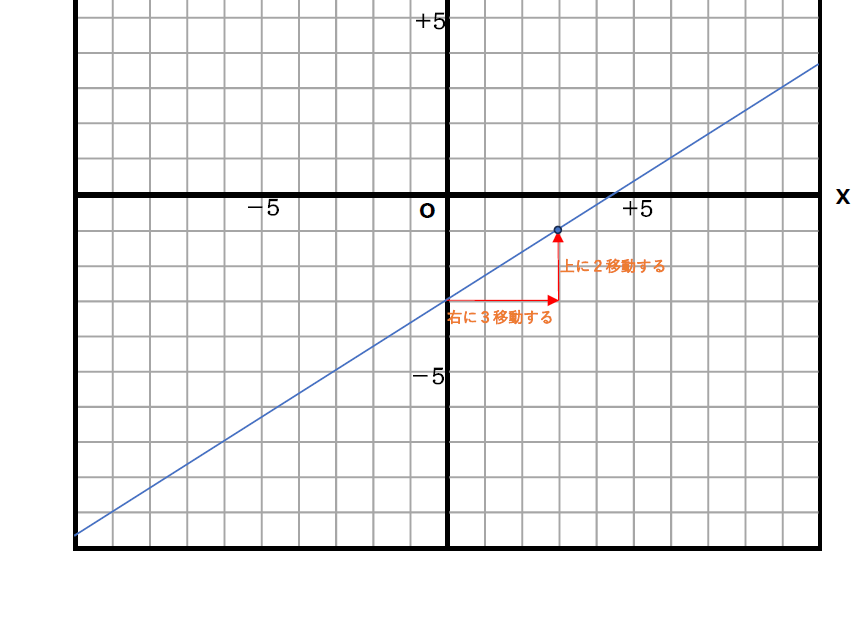

さっきの座標までは右(\(\displaystyle x\))に「3」
上(\(\displaystyle y\))に「2」進んでいるから
3÷2で答えが出るんだ!

惜しい!!!!!!
皆さんはわかりましたか?
もう一度振り返っておきましょう。
上下(\(\displaystyle y\))に進んだ数÷右(\(\displaystyle x\))に進んだ数
です。
覚えていますか?
\(\displaystyle 変化の割合(a)=\frac{yの増加量}{xの増加量}\)
上下に進んだ数は「2」
右に進んだ数は「3」なので
この問題は2÷3が正解です。

カエデ先生、2÷3はできません。

いい質問だね。
でも、数学には「割り切れない」なんてことは絶対にないんです。
※中学の数学で小数の答えはほぼ必要ありません!!!!
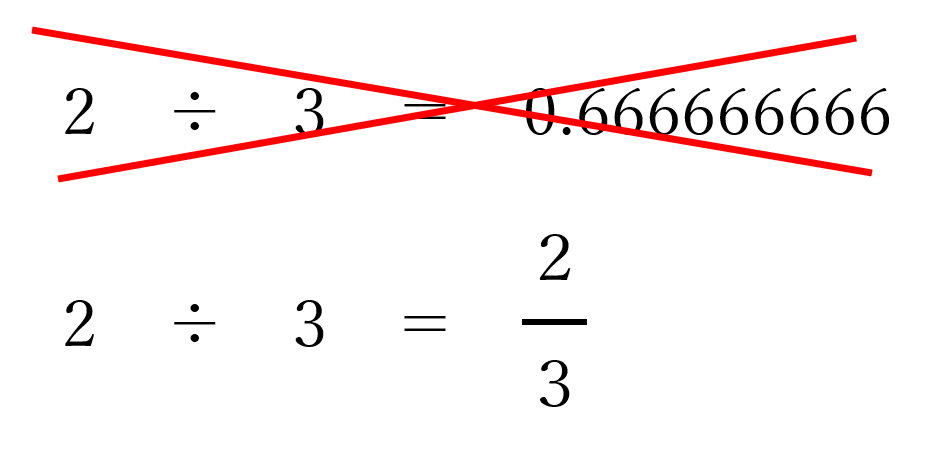
なぜかというと、
割り算は分数で表すことができるからです。
小数で表そうとすると、
どうしても割り切れないものが
出てきてしまいます。
それをおよその数(概数)で「0.66!」
と答えても不正解
になってしまいます。
では分数であればどうでしょう?
約分が必要なときもありますが、
必ず正確な答えになるのです!
\(\displaystyle a=2÷3=\frac{2}{3}\)
と考えられるよう特訓が必要ですね。
これで\(\displaystyle a=-\frac{2}{3}\)、\(\displaystyle b=-3\)
というところまでわかりました。
この式を\(\displaystyle y=ax+b\)
に代入すれば終了です!
\(\displaystyle y=-\frac{2}{3}x-3\)
ここまでついてこれましたか?

わかった!
自分でやってみたいから、先生問題出して!

そうですね。
一発で理解できたのであれば、
さっそく練習問題やってみますか!
練習問題に挑戦しよう!
まとめ
今回のまとめ
グラフから式を求めるときはまず切片を見つける。→bが決まる
次に切片以外の座標を見つけて切片から【\(\displaystyle y\)に進んだ数÷\(\displaystyle x\)に進んだ数】→\(\displaystyle a\)が決まる
※割り算の答えは小数にしないで分数にすること。
2つの値を\(\displaystyle y=ax+b\)に代入すれば完了!



コメント